FFT 详解

前方高能！

0. 前言

本节是数学之中算非常难的模板题了。

注意，如果有没学过的知识点，请记住结论即可，不必深挖使自己绕晕。

1. 解决问题

求两个高次多项式的乘积。

设 $A(x)$ 多项式为 $n$ 次，$B(x)$ 多项式为 $m$ 次（$n\geq m$）。

朴素复杂度为 $O(nm)$，该算法可以在 $O(n\log n)$ 的时间求出。

2. 主要方法

1）前置知识

A. 点值表示

任意一个 $n$ 次多项式都可以用任意 $n+1$ 个点来表示，其中 $n+1$ 个点都在函数上。

证明不难，就是 $n+1$ 个 $n+1$ 元一次方程有唯一解。

经过“范德蒙矩阵”的行列式推导，当且仅当 $x_i\not=x_j(i\not=j)$ 时原方程有唯一解。

B. 复数的基本运算

首先，令 $i=\sqrt{-1}$。

所以，所有的复数都可以表示为 $a+bi$。

复数的加法：$(a+bi)+(c+di)=(a+c) +(b+d)i$。

用向量的角度看，就是两个向量的合成。

复数的乘法：$(a+bi)\times(c+di)$$=(ac-bd)+(ad+bc)i$。

从向量的角度看，乘积的模就为原来的向量的模的乘积。

乘积的角度为 $\theta=\theta_1+\theta_2$。$\theta$ 为向量与 x 轴正半轴的夹角。

C. 复数域上的单位根

画一个单位圆。

将该圆划分为 $n$ 份，从 $x$ 轴正半轴逆时针取了 $k$ 份后，终边所表示的向量记为 $\omega_n^k$。

$n$ 次单位根为：$\omega_n^k(k\in [0,n-1])$。

它有几个性质：

1. $\forall i\not=j,\omega_n^i \not=\omega_n^j$。
2. $\omega_n^k=\cos\dfrac{2k \pi}{n}+\sin\dfrac{2k\pi}{n}i$。
3. $\omega_n^0=\omega_n^n=1$。
4. $\omega_{2n}^{2k}=\omega_n^k$。
5. $\omega_n^{k+\frac{n}{2}}=-\omega_n^k$。

同样，具有上述几个性质的点也是 $n$ 次单位根。

2）核心：点值表示与系数表示的转换

在 FFT 中，我们一共取 $n+m+1$ 个点。

怎样求出 $C(x)$ 的表达式？

我们设定 $n+m+1$ 个点，然后求出每一个点的函数值，就求出了点值表示。

怎样转换为系数表示呢？

首先，我们考虑取哪些点。

对于 $A(x)$ 来说，我们取 $\omega_n^k (k\in[0,n-1])$ $n$ 个横坐标。

我们还是首先考虑怎样从系数表示转换为点值表示。

然后，我们按次数分类，分为奇数次和偶数次。

$A(x)=a_0+a_1x+a_2x^2+…+a_{n-1}z^{n-1}$。

假设 $n$ 为偶数。

$A_1(x)=a_0+a_2x+a_4x^2+…+a_{n-2}x^{\frac{n}{2}-1}$。

$A_2(x)=a_1+a_3x+a_5x^2+…+a_{n-1}x^{\frac{n}{2}-1}$。

所以，我们惊喜地发现：$A(x)=A_1( x^2)+xA_2(x^2)$！

然后我们将 $\omega_n^k$ 代入，得到：

如果 $k\in[0,\dfrac{n}{2}-1]$，原式可以写成：

$$\begin{aligned} A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k}) \\=A_1(\omega_{\frac{n}{2}}^k)+\omega_n^kA_2(\omega_{\frac{n}{2}}^k) \end{aligned}$$

如果 $k\in[\dfrac{n}{2},n-1]$，原式可以写成：

$$A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})\\=A_1(\omega_n^{2k-n})-\omega_n^{k-\frac{n}{2}}A_2(\omega_n^{2k-n})$$

这样，我们就可以在 $O(n\log n)$ 的时间内从系数表示转换到点值表示。

下面，我们进行逆变化：从点值表示转换到系数表示。

假设最终的答案为 $A(x)=c_0+c_1x+…+ c_{n-1}x^{n-1}$。

结论：

$$c_k=\dfrac{\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i}{n}$$

其中，$y_i$ 表示最终得到的纵坐标。

首先，我们假设该结论成立。

再定义 $B(x)=y_0+y_1x+y_2x^2+…+y_{n-1}x^ {n-1}$。

不难发现 $c_i=B(\omega_n^{-i})$。

所以，我们相当于把 $B$ 从系数表示法转换为点值表示法，就在做一次前面的即可。

可以发现（？），有一个负号不影响答案。

好，下面我们来证明该结论。

证明：（从结论反推）

$$n*c_k=\sum_{i=0}^{n-1}y_i(\omega_{n}^ {-k})^i\\=\sum_{i=0}^{n-1}(\sum_{j= 0}^{n-1}c_j(\omega_{n}^{i})^j)(\omega _{n}^{-k})^i$$ $$\begin{aligned} =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}c_j (\omega_{n}^{i})^j(\omega_{n}^{-k})^i \\=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1} c_j(\omega_{n}^{j-k})^i \end{aligned}$$ $$=\sum_{j=0}^{n-1}c_j(\sum_{i=0}^{n-1} (\omega_{n}^{j-k})^i)$$

在最里面的括号 $(\omega_{n}^{j-k})^i$，$j,k$ 都是常量，$i$ 是变量，所以我们可以再构造 $D(x)=\sum _{i=0}^{n-1}x^i$，原式就可以化成：

$$=\sum_{j=0}^{n-1}c_j*D(\omega_{n}^{j-k})$$

接着，我们讨论 $D(\omega_{n}^{x})$ 的取值：

$x\not=0$：，首先，$D(\omega_{n}^{x})= \omega_{n}^{0}+\omega_{n}^{x}+ \omega_{n}^{2x}+…+\omega_{n} ^{(n-1)x}$。

其次，$\omega_{n}^{x}D( \omega_{n}^{x})=\omega_{n}^{x}+ \omega_{n}^{2x}+…+\omega_{n} ^{(n-1)x}+(\omega_{n}^{nx}=0)$。

发现，这两项相等。

于是，$(\omega_{n}^{x}-1)D(\omega_{n}^{x})=0$，又 $x\not=0$，所以 $\omega_{n}^{x}\not=1$，于是 $D(\omega_{n}^{x})=0$。

$x=0$：$D(\omega_{n}^{x})=D(1)=n$。

所以，当 $j\not=k$ 时，原式为 $0$。

带入原式，便可以得到：

$$=nc_k$$

证毕。

现在，我们讨论的是怎样求出 $n$ 次单位根对应的点值。

首先，有前面推导的式子：

$$A(\omega_{n}^{k})=A_1(\omega_{\frac{n}{2}}^{k})+\omega_{n}^{k}A_2(\omega _{\frac{n}{2}}^{k})\\A(\omega_{n}^{ k+\frac{n}{2}})=A_1(\omega_{\frac{n} {2}}^{k})-\omega_{n}^{k}A_2(\omega _{\frac{n}{2}}^{k})$$

在实践中，递归的常数较大，我们使用迭代。

首先，我们发现，如果 $i\leq\dfrac{n}{2}$，就可以得到 $a_i=b_i+\omega_{n}^ic_i$，如果 $i>\dfrac{n}{2}$，就可以得到 $a_i= b_i-\omega_{n}^{i-\frac{n}{2}}c_i$，其中 $b_i,c_i$ 分别表示左边和右边求出来的系数，分别对应偶数求出来的点值和奇数次方求出来的点值。

我们每一次求点值时，会递归并将偶数次项的放前面，将奇数次项的放后面，然后计算出前后的 $n$ 次方根的数值，然后将答案合并即可。

来看一张图。

（红色 $a$ 表示系数的长度，蓝色 $b$ 表示已经求出的点值的合并，黑色表示点值的转移）

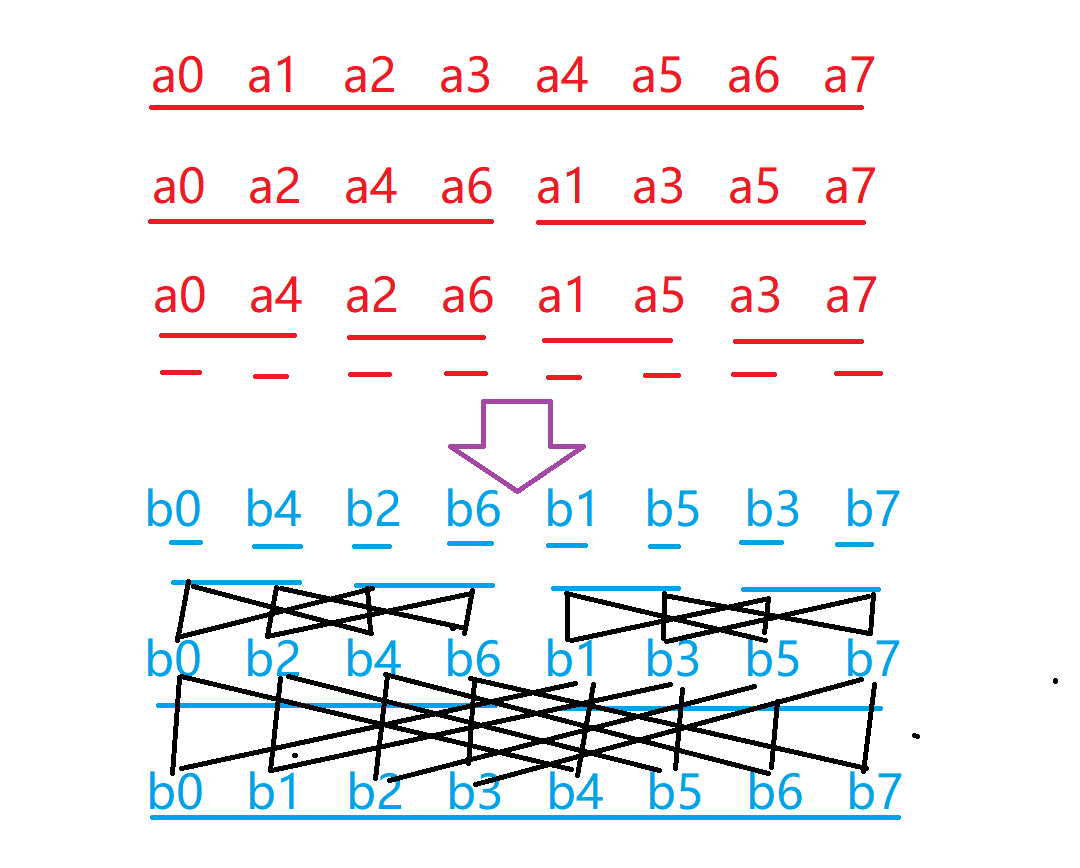
首先，我们要预处理第一层，即 $b$ 的最上面一层。

我们找一下规律：第零个 $0$，第一个 $4$，……

可以发现，答案求出的就是二进制的翻转，这个例子中是指三位的异或。

我们考虑刚才的结论怎么证明。

其实很简单：如果最后一位为 $1$，则放在右边，也就是当前的最高位为 $1$，也就是翻转了。

假设 $bit$ 位的翻转，我们怎样求出翻转结果呢？

记要翻转的数为 $i$，结果为 $\text{rev}(i)$。

首先，我们将最后一位不看，即为 $i/2$，然后将剩下的翻转，为 $\text{rev}(i/2)$，然后在最前面补上前面的最后一位。

所以，我们可以得到一个递推公式：rev[i] = (rev[i >> 1]) | (i & 1) << (bit - 1)。

至此，所有的推导全部结束。

大功告成！！！

最后的最后，我们总结一下整体的思路。

首先，将两个式子分别从系数表示转换为点值表示，其中要使用到递归（或迭代）求点值，最后用两边合并为当前，时间复杂度为 $O(n\log n)$。

然后，用点值表示将两个式子乘起来，直接得到 $O(n)$。

然后，我们将得到的式子用一个证明，即为点值做系数，$\omega_{n}^{-k}$ 做自变量，就可以求出 $n*c_k$ 的值，这再做一次前面的正向即可。

最后，除以 $n$ 输出即可。

至此，上代码。可能还是有一些地方没有讲清楚，请读者看代码吧（逃

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

const int N = 3e6 + 10;
const double PI = acos(-1);

struct Complex{
    double x, y;
    const Complex operator +(const Complex &t)const{
        return (Complex){x + t.x, y + t.y};
    }
    const Complex operator -(const Complex &t)const{
        return (Complex){x - t.x, y - t.y};
    }
    const Complex operator *(const Complex &t)const{
        return (Complex){x * t.x - y * t.y, x * t.y + y * t.x};
    }
}a[N], b[N];
int tot, bit, rev[N];

void FFT(Complex a[], int inv)
{
    for (int i = 0; i < tot; ++ i)
        if (rev[i] < i) swap(a[rev[i]], a[i]);

    for (int mid = 1; mid < tot; mid <<= 1)
    {
        Complex w1 = (Complex){cos(PI / mid), sin(inv * PI / mid)};
        for (int i = 0; i < tot; i += mid * 2)
        {
            Complex now = (Complex){1, 0};
            for (int j = 0; j < mid; j ++, now = now * w1)
            {
                Complex x = a[i + j], y = now * a[i + j + mid];
                a[i + j] = x + y, a[i + j + mid] = x - y;
            }
        }
    }
}

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 0; i <= n; ++ i) scanf("%lf", &a[i].x);
    for (int i = 0; i <= m; ++ i) scanf("%lf", &b[i].x);

    while ((1 << bit) < n + m + 1) bit ++;
    tot = 1 << bit;

    for (int i = 0; i < tot; ++ i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1);

    FFT(a, 1);FFT(b, 1);
    for (int i = 0; i < tot; ++ i) a[i] = a[i] * b[i];
    FFT(a, -1);

    for (int i = 0; i <= n + m; ++ i) printf("%d ", int((a[i].x / tot) + 0.5));

    return 0;
}