mydcwfy's Blog

仙人掌

Posted on
Symbols count in article: 5.8k Reading time ≈ 13 mins.

同步发表于 P5236 题解。

0. 前置知识

本蒟蒻也是最近学习这个 巨毒瘤 的算法，好多地方也是一头雾水，仔细想了几个晚自习后，有些恍然大悟，于是写了这篇题解。

需要的东西：Tarjan（似乎没有具体的模板）。

就是一个求边强连通分量的算法，一会我们要利用它并改进为我们所用。

还有一颗看完我的博客的心~~

1. 圆方树

其实，圆方树就是将环的作用转化为一棵树的作用，使原来的图变为了新图，许多性质没有变化，但处理树会简单许多。

以例题为例：题目传送门

想一想，怎样将环变为树的样子？

回归定义的一个特殊性质：

任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。

翻译成人话（？），就是原图由一些边不相交的环和另外的边构成。

首先，可以想到的是，将一个环缩为一个点，将整个图缩为一棵树（因为无向图中只有树和环两种形状，没有第三种，又因为没有环套环（边重合），所以一定变为一棵树）。

但是，环内的边和点间的距离就没法统计了。

我们假设任意一个点为根，那么一定会有一个点距离根节点最近。

来看一个图（ 盗的例题的图 ）

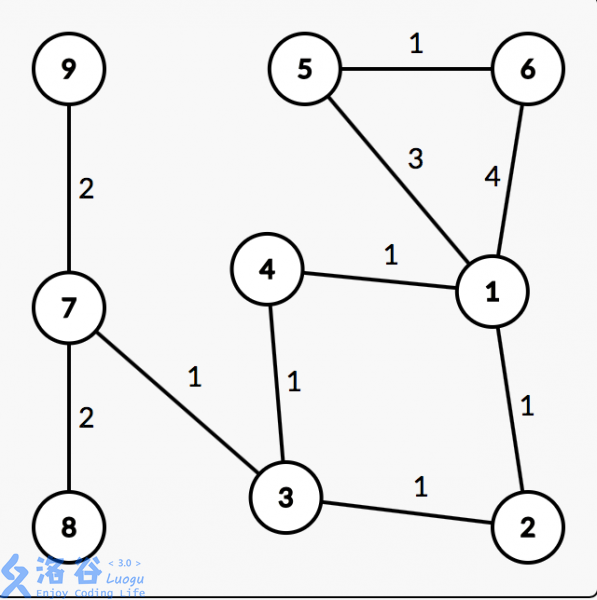
假设七号点为根，那么，对于 “1-2-3-4” 的环，三号点距离根节点最近。

我们设最近的点具有 “A” 性质。

下面，我们证明一个东西：环内的点到根节点一定经过环内具有 “A” 性质的点。

显然，如果不经过该点的话，就不可能达到根节点。

那么，如果在树中，该点如果想向上走的话，必须经过该环的 “A” 节点。

我们就可以考虑将这种关系转化为树的节点之间的关系。

环内的节点通向 “A” 节点只可能有两条路径：顺时针和逆时针。

又由于对于每一个点，长的一条路肯定用不上，那么我们只需要存到 “A” 节点的最短距离即可。

那么，原图很大程度上就等价于新图了。

但是，对于一些题来说，我们需要判断原来的边还是环中的边变换过来的。

那么，我们可以使用 “圆方树”。

假设原来的点叫做圆点，新建的点叫做方点。

对于环内的节点，我们可以新建一个方点，向 “A” 的点连接一条权值为 0 的边，在从新点到其他点连接原来应有的权值。

现在，我们判断是不是原来的边，只需判断是不是有新建的点即可。

举个例子，上面的仙人掌建为圆方树（7 号是根节点）是：

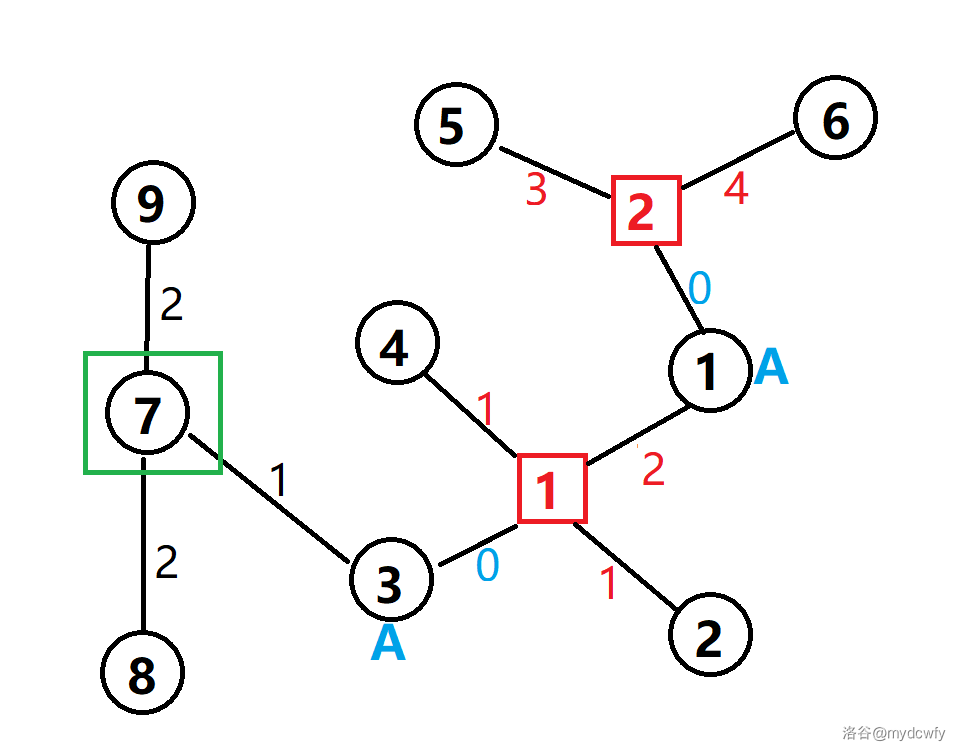
2. Tarjan 算法及变形

我们刚才讨论的范围，是在能求简单环的基础上，现在，我们的问题是，如何才能找到所有的简单环？

可能大家都会想到，直接用 Tarjan 算法，就可以去求了。

但是，有一个问题：Tarjan 求的是边双联通分量，即去掉任意一条边后，原图仍然联通，那么，原图的 “123456”6 个点，满足该要求，但他们并不属于同一个简单环，怎么办呢？

于是，需要我们改进该算法。

首先，我们回顾一下原算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//来自本人缩点模板题
void Tarjan(int x)
{
	dfn[x]=low[x]=++tot;
	st[++top]=x, ins[x]=true;
	for (int i=h[x];~i;i=ne[i])
    	if (!dfn[e[i]])
    	{
    		Tarjan(e[i]);
			low[x]=min(low[x],low[e[i]]);
    	}
		else if (ins[e[i]]) low[x] = min(low[x], dfn[e[i]]);
	if (low[x]!=dfn[x]) return;
	cnt++;int now;
	do{
		now=st[top--];
		ins[now]=0; 
		bel[now]=cnt;
	}while (now!=x);
	return ;
}

原算法中，只要还在栈中，我们都将所有归为一个边双联通分量。

但是，现在，如果我们还遇到这种情况的话，就应该一个一个的处理为一个一个的简单环，而不是揉在一起。

所以，当我们遇到 $low[e[i]]<dfn[x]$ 的时候，我们直接倒回去，就可以倒推出一整个环的情况了。

请注意，此时 $x$ 也为其中的点。

具体来说，我们遇到这种情况时，直接 $\operatorname{build-round-square}(x,e[i],w)$，表示从 $e[i]$ 倒推，直到 $x$ 为 “A” 点，其中 $(x,e[i])$ 的权值为 $w$。

具体来说，我们遇到了这样的情况：

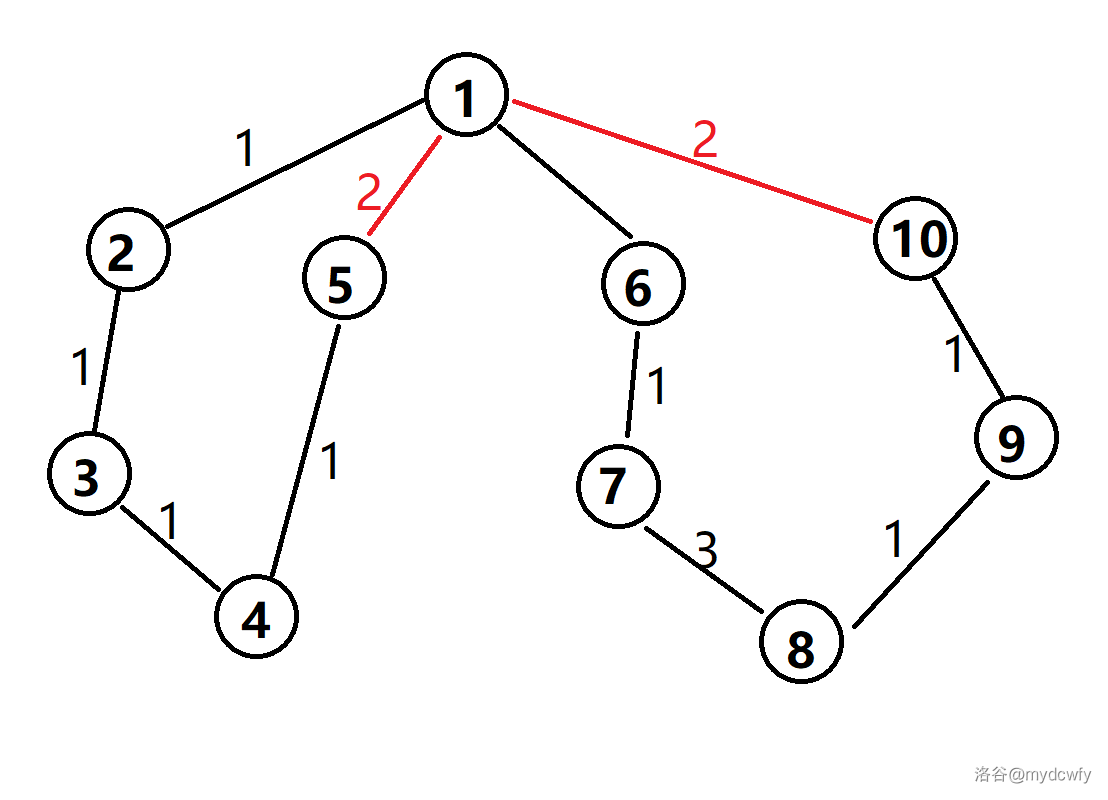
（好像少标了一条边的权值）

我们知道，Tarjan 算法建了一棵搜索树，在树上进行计算。

如图，黑边就是搜索树的边，而红边就是非树边。

肉眼可见，有两个环。

对于每个节点，我们维护他在搜索树中的父亲，还有到父亲的距离。

如果相连的节点在他的下面（即不是父亲），并且他的父亲不是该节点，说明有另外一条路径（树边）可达他的儿子，我们就可以 $\operatorname{build-round-square}(x,e[i],w)$ 了。

举个例子，搜索完 1 节点后，我们找连接点，找到 5 号点，发现满足上面的性质，于是就 $\operatorname{build-round-square}(1,5,2)$ 即可以了。

如果你还感到费解，请看前面的例图，加以理解。

如果你对传参有不理解，看一下代码就知道了。

于是，我们就可以得到这样的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void add(int h[],int a,int b,int c)
{
    e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}

void build_round_square(int x,int y,int w)
{
    int sum=w;
    for (int i=y;i!=x;i=fa[i])
    {
        // cout<<i<<' ';
        s[i]=sum;
        sum+=fw[i];
    }
    stot[x]=s[x]=sum;
    add(h2,x,++square_node,0);
    for (int i=y;i!=x;i=fa[i])
    {
        stot[i]=sum;
        add(h2,square_node,i,min(s[i],stot[i]-s[i]));
    }
}

void tarjan(int x,int from)
{
    dfn[x]=low[x]=++tot;
    for (int i=h1[x],j;~i;i=ne[i])
        if (!dfn[j=e[i]])
        {
            fa[j]=x,fw[j]=w[i];
            tarjan(j,i);
            low[x]=min(low[x],low[j]);
            if (low[j]>dfn[x]) add(h2,x,j,w[i]);
        }
        else if (i!=(from^1)) low[x]=min(low[x],dfn[e[i]]);
    for (int i=h1[x],j;~i;i=ne[i])
        if (dfn[j=e[i]]>dfn[x]&&fa[j]!=x)
            build_round_square(x,j,w[i]);
}

3. 回归本题

1）题意

  1. 给定一个仙人掌图，有 $Q$ 次询问，询问 $u$ 和 $v$ 之间的最短路。
  2. $n,q\leq10^4,m\leq2*10^4,w\leq10^5$。

2）具体算法

前面的东西是总体的仙人掌转圆方树的算法，对于不同的题来说，肯定也会有一些细节不同。

当然，仙人掌的题的大概思路是：

  1. 将仙人掌转化为圆方树。
  2. 结合其他树的算法（树链剖分，点分治等），将本题树的写法写好。
  3. 分情况，看是圆点还是方点，进行算法调整。

本题也是如此。

考虑树上怎么做。

很明显，使用倍增算法，将一个节点的 $2^k$ 次祖先存储下来。

再利用前缀和的思想，答案即为：$ans=d[a]+d[b]-2d[lca]$。

现在，我们考虑分类讨论。

首先，假设 $lca$ 是圆点，直接按上面求即可（因为会在原来的点相会）。

假设 $lca$ 是方点呢？

这说明，当到了 $lca$ 的前一层时，两个点是在同一个环上。

对于每一个节点，可以存储一个前缀和 $s[]$，即从 “A” 性质的点按同一个方向（指一个环中是同一个方向）走到该点的距离。

特别地，”A” 性质的点记为环的总权值。

现在我们可以将环间的路径表示为（$x,y$ 分别表示 $a,b$ 环里的节点）：$d=\min(|s[x]-s[y]|,stot[x]-|tot - |s[x] - s[y]||)$。

现在我们就可以完美的解决了。

4. 代码

还会有一些细节从代码中呈现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=2e4+10,M=1e5+10,L=14;

int h1[N],h2[N],e[M],ne[M],w[M],idx,square_node;
/*
h1,h2分别表示原图和新图的节点的头指针
square_node表示新建的点 
*/
int dfn[N],low[N],tot;//Tarjan 算法 
int stot[N],s[N],fa[N],fw[N];
/*
stot表示所在环的总权值
s是前缀和 
fa即为搜索树中的父亲
fw表示到父亲的距离 
*/
int f[N][L+1],depth[N],dis[N];//倍增算法 
int n,m,q,A,B;//A,B表示走到同一个环中的节点 

void add(int h[],int a,int b,int c)
{
    e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}

void build_round_square(int x,int y,int w)
{
    int sum=w;
    for (int i=y;i!=x;i=fa[i])
    {
        // cout<<i<<' ';
        s[i]=sum;
        sum+=fw[i];
    }
    stot[x]=s[x]=sum;//注意s[x]要赋值为总权值 
    add(h2,x,++square_node,0);
    for (int i=y;i!=x;i=fa[i])
    {
        stot[i]=sum;
        add(h2,square_node,i,min(s[i],stot[i]-s[i]));
    }
}

void tarjan(int x,int from)
{
    dfn[x]=low[x]=++tot;
    for (int i=h1[x],j;~i;i=ne[i])
        if (!dfn[j=e[i]])
        {
            fa[j]=x,fw[j]=w[i];
            tarjan(j,i);
            low[x]=min(low[x],low[j]);
            if (low[j]>dfn[x]) add(h2,x,j,w[i]);
        }
        else if (i!=(from^1)) low[x]=min(low[x],dfn[e[i]]);
    for (int i=h1[x],j;~i;i=ne[i])
        if (dfn[j=e[i]]>dfn[x]&&fa[j]!=x)//Tarjan算法改进 
            build_round_square(x,j,w[i]);
}

void dfs(int x,int fa)//倍增算法预处理 
{
    depth[x]=depth[fa]+1;
    f[x][0]=fa;
    for (int i=1;i<=L;++i) f[x][i]=f[f[x][i-1]][i-1];
    for (int i=h2[x];~i;i=ne[i])
        if (e[i]!=fa)
        {
            dis[e[i]]=dis[x]+w[i];
            dfs(e[i],x);
        }
}

int LCA(int a,int b)
{
    if (depth[a]<depth[b]) swap(a,b);
    for (int i=L;i>=0;--i)
        if (depth[f[a][i]]>=depth[b]) a=f[a][i];
    if (a==b) return a;
    for (int i=L;i>=0;--i)
        if (f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
    A=a,B=b;
    return f[a][0];
}

int main()
{
    memset(h1,-1,sizeof h1);
    memset(h2,-1,sizeof h2);
    scanf("%d %d %d",&n,&m,&q);
    int a,b,c;
    while (m--)
    {
        scanf("%d %d %d",&a,&b,&c);
        add(h1,a,b,c);add(h1,b,a,c);
    }
    square_node=n;
    tarjan(1,-1);
    dfs(1,0);
    while (q--)
    {
        scanf("%d %d",&a,&b);
        int lca=LCA(a,b);
        if (lca<=n) printf("%d\n",dis[a]+dis[b]-2*dis[lca]);
        else{
            int res=dis[a]-dis[A]+dis[b]-dis[B];
            res+=min(abs(s[A]-s[B]),stot[A]-abs(s[A]-s[B]));
            printf("%d\n",res);
        }
    }
    return 0;
}