自认为写得还行。
0. 前言
本文不比前面的学习笔记 后缀自动机笔记,这篇文章大概能保证你能理解。
本文同样不会给出证明,但是会亲近读者,尽可能让读者看懂。
图片建议新标签页打开看一下。因为用的是 Luogu,github 上会挂。
1. 职能
这个就是一个可以快速查找一个字符串的子串,1 号点是根节点,走 1 号点可以走到所有的子串。
预处理和寻找都是线性 $O(n)$ 的。
2. 前置知识
$\text{endpos}$ 的一些基本定义和性质。
顾名思义,$\text{endpos}$ 对于字符串中的一个子串而定义,是指所有出现的地方的最后一个字符的位置。
(可能有些绕,看一下下面的解释
首先,我们定义,$\text{endpos}$ 相同的作为一个等价类,可以看做同一个状态,对应在 SAM 中是同一个结点。
比如,我们还是来看一个实例 $\texttt{abcbc}$:
- $\{\texttt{abcbc},\texttt{bcbc},\texttt{cbc} \}$ 的 $\text{endpos}$ 都是 $\{5\}$。
- $\{\texttt{bc},\texttt{c} \}$ 的 $\text{endpos}$ 都是 $\{3,5\}$。
当然没有列举完,读者可以自己推一下(?
可以发现,$\text{endpos}$ 有一个性质,就是如果 $\text{endpos}$ 相同的,一定是长度递减的字符串。
还是看上面的实例:
- $\{\texttt{abcbc},\texttt{bcbc},\texttt{cbc} \}$ 是长度递减的字符串,且后面一个是前面一个的后缀。
- $\{\texttt{bc},\texttt{c} \}$ 是长度递减的字符串,且后面一个是前面一个的后缀。
现在,大概理解了 $\text{endpos}$ 的基本性质了吧。
3. SAM 的构造
这里我们先贴代码。
1 | struct Node |
主函数调用的时候,直接 for (int i = 1; str[i]; ++ i) extend(str[i] - 'a'); (这里假设只有小写字母)。
可以先背代码,再看下面的讲解。
下面一点一点的讲解:
1 | struct Node |
说明一下每一个变量的含义:
tr[N]:前面所讲的 $\text{endpos}$ 相同的子串将会被放入同一个结点,也就是说这些子串遍历时会走到这个结点停止。
ch[26]:指所有的结点的转移。
len:指所有的子串的最大长度。
fa:可以看做 fail,也就是匹配失败的时候会走到哪个结点(现在大概用不到,有点像 KMP)。
性质:$fa$ 指向的结点的最长长度就是当前结点所代表的子串的最短长度减 1。
还是拿 $\texttt{abcbc}$ 来说:
$\{\texttt{abcbc},\texttt{bcbc},\texttt{cbc} \}$ 的最短长度是 3,那么这个结点的 $fa$ 是 $\texttt{bc}$ 所在的结点, 长度为 2。
这里有一些重要,请务必理解。(其实认真读一下上面的定义就可以了)
然后,还有一个重要的性质:如果当前所代表的最长子串是 $s$,那么按照 $fa$ 一直跳的话,所有遍历到的结点所代表的子串一定都是 $s$ 的后缀,且 $s$ 的后缀一定都被遍历到。
拿 $\{\texttt{abcbc},\texttt{bcbc},\texttt{cbc} \}$ 为例:这个结点的 $fa$ 会指向 $\texttt{bc}$ 所在的结点,然后 $\{\texttt{bc},\texttt{c}\}$ 是一个结点,然后 $fa$ 是 $\varnothing$。可以发现,整个遍历到的是 $\{\texttt{abcbc,bcbc,cbc,bc,c},\varnothing \}$,恰好是 $\texttt{abcbc}$ 的后缀的所有。
last = tot = 1:这里表示开始已经有了一个节点,我们定义最开始结点的 $fa$ 是 0,长度也是 0。
int p = last, np = ++ tot; ...; last = tot;:$p$ 表示前面的结点,$np$ 表示当前的结点,处理完当前结点的时候要将 $last$ 更新。
for (; p && !tr[p].ch[c]; p = tr[p].fa) tr[p].ch[c] = np;
根据刚才的性质:
如果当前所代表的最长子串是 $s$,那么按照 $fa$ 一直跳的话,所有遍历到的结点所代表的子串一定都是 $s$ 的后缀,且 $s$ 的后缀一定都被遍历到。
有了这个结论的话,这里就比较简单了:直接一直按照 $fa$ 跳,将所有的结点都加上当前字符 $c$。
为什么要加上 !tr[p].ch[c] 呢?
因为如果出现了相同的字符,我们就有可能出现 $\text{endpos}$ 不是当前结点的,我们要特殊处理。
这个稍微有点复杂,现在可以理解为有原来的指向了,如果再赋值就会导致一些被覆盖,我们等一下再讲。
if (!p) tr[np].fa = 1;:这个说明程序退出循环是因为 $p=0$,所以说明 $last$ 结点所代表的最长子串,也就是原串(每一次扩展时 $last$ 都赋值给了最新的那个,也就是最长的那个),原串的所有后缀都加了当前字符 $c$,然后到了 $np$ 这个结点。
所以,$np$ 所代表的子串的长度一定从 $1$ 到最长长度。
比如,原来的串是 $\texttt{abc}$,加上了 $\texttt{d}$,那么 $\texttt{abc},\texttt{bc},\texttt{c},\varnothing$ 都会加上 $d$ 这个字符。
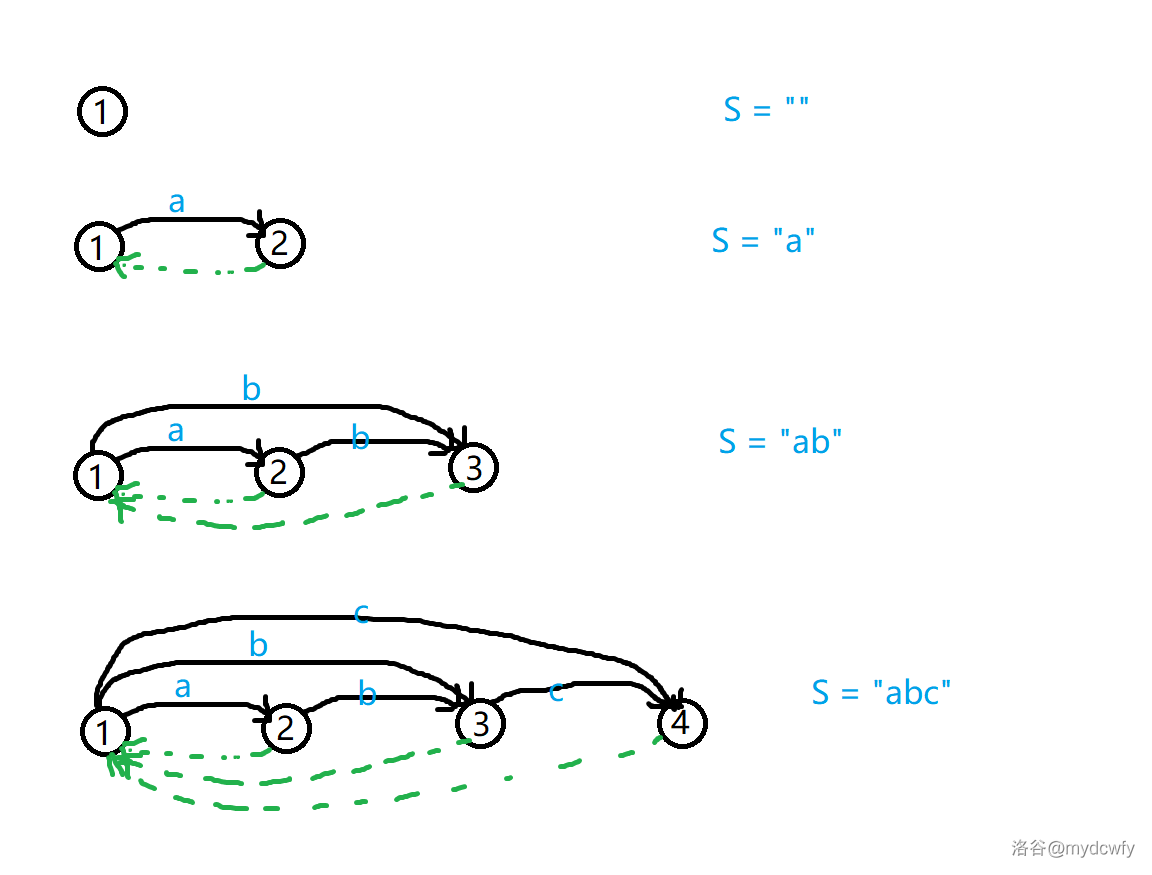
(黑色边代表 $ch[]$,绿色边代表 $fa$)
前面没有理解可以看一下这个图。
那么,$np$ 的 $fa$ 就是长度为 $0$ 的串在的结点,也就是 $1$。
1 | int q = tr[p].ch[c]; |
这里就有些难理解了,我们首先填一下前面的坑。
因为 $p$ 既可以转移到 $q$,也可以转移到 $np$,那么可以得到结论:$p$ 转移的 $ch[c]$ 有两个出现。
这里我们用一下前面的例子,在前面的基础 $\texttt{ab}$ 加上 $\texttt{b}$。
当循环到 $p=1$ 的时候,我们发现已经有了 $b$ 的转移边,这意味着 $\varnothing+\texttt{b}$ 已经出现了一次,这里又一次出现了,也就是说,$\text{endpos}$ 结果是不同于 $q$ 本身的 $\text{endpos}$ 了,所以要特殊处理。
这里明显是遇上了也有 $c$ 转移的。
我们首先记录下 $ch[c]$ 的位置 $q$。
首先,为什么 tr[q].len = tr[p].len + 1 与 tr[q].len != tr[p].len + 1 是不同的呢?
画一个图。
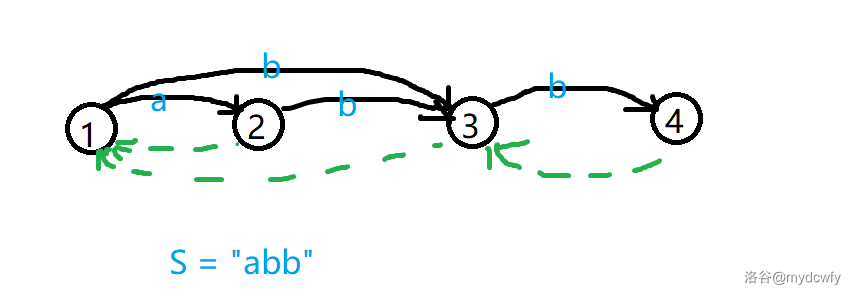
根据前面所讲,$\texttt{b}$ 的 $\text{endpos}$ 是 $\{2,3\}$,不同于原来 3 号结点的 $\text{endpos}$。
但是,这里判断的 tr[q].len = tr[p].len + 1 是什么意思呢?
前面讲到,$len$ 的意思是一个结点所代表的子串的最长长度。
如果 tr[q].len == tr[p].len + 1 的话,那么这里只有长度为 $tr[q].len$ 的一个子串!
所以我们可以直接将这个结点的 $\text{endpos}$ 改为新的子串。
比如说,前面的 $q=3$ 的 $\text{endpos}$ 为 2,但是又添加了 $b$ 这个字符,我们就将 $q=3$ 的 $\text{endpos}$ 直接改为 $\{2,3\}$ 就可以了。
很明显,3 号结点所代表的子串仍然是 $\{\texttt{ab},\texttt{b}\}$,然后 $np=4$ 所代表的子串是 $\{\texttt{abb}\}$,比较明显,4 的 $fa$ 是 3。
(你以为完了?还多着呢
1 | int nq = ++ tot; |
这里是前面情况的相反情况,也就是 tr[q].len != tr[p].len + 1。
那么,我们这里就需要将 $q$ 结点拆为两个结点。
其中一个仍然是 $q$,另一个是 $nq$,也就是新建结点。
我们再画一个图,建的是 $\texttt{abcb}$ 的后缀自动机。
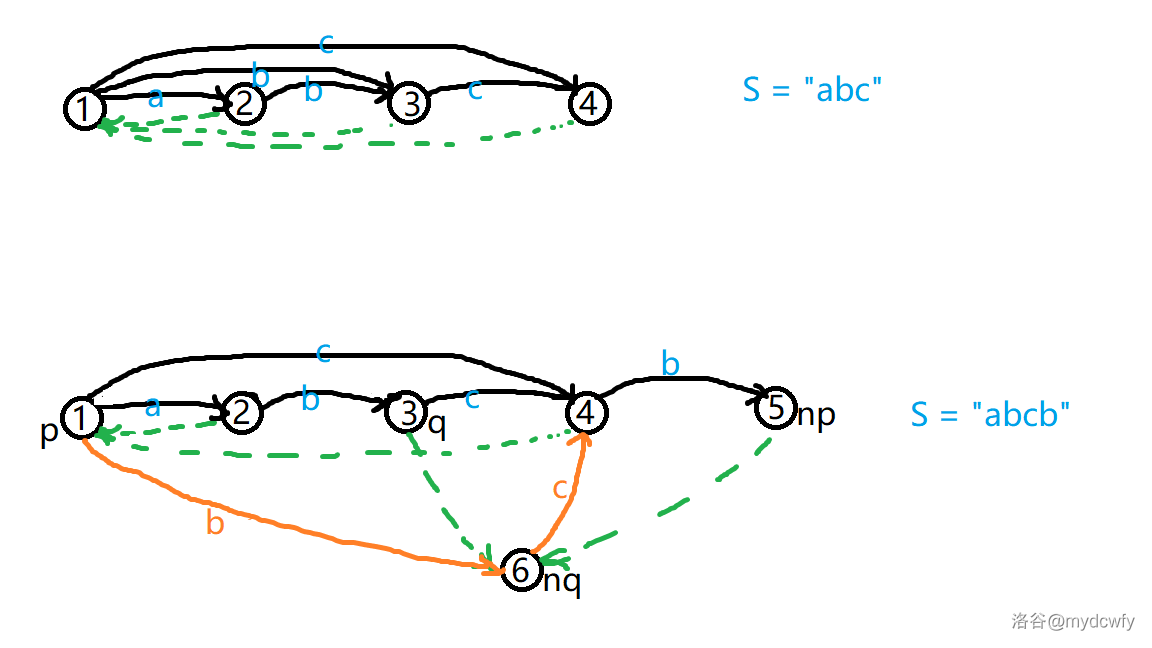
tr[nq] = tr[q]:这一个比较简单,因为就是复制过来即可。
tr[nq].len = tr[p].len + 1:这里是指将 $q$ 的长度为 $tr[p].len+1$ 的子串。
tr[q].fa = tr[np].fa = nq:首先,我们从例子中学习。
很明显,$q$ 的最短子串是 $\texttt{ab}$,也就是长度减 1 的就是 $\texttt{b}$,同理,$np$ 的最短子串是 $\texttt{cb}$,长度减 1 也是 $\texttt{b}$。
再从证明入手。
前面说到,$nq$ 这个结点是从 $q$ 这个结点分离出来的,且是最短的子串被分离了的。
所以,$q$ 的 $fa$ 就应该是 $q$,这个显然 (显然大法)。
然后,因为 $np$ 本来应该也是有 $nq$ 这个结点所代表的子串的。
那么,我们也可以说 $nq$ 是从 $np$ 分离出来的。
所以,这一句显然。
for (; p && tr[p].ch[c] == q; p = tr[p].fa) tr[p].ch[c] = nq;
这里是指,既然 $p$ 这个结点所代表的最长子串都是重复了的,那么 $p$ 的所有 $fa$(前提是原来是 $tr[p].ch[c] == q$)都应该有 $ch[c]$ 指到 $nq$ 这个结点。
看一下上面的例子。
$p$ 所代表的是 $\varnothing$,它接上 $\texttt{b}$ 也应该属于 $nq$,所以 $tr[p].ch[‘b’-‘a’]=nq$。
$p$ 的 $fa$ 是 0,所以结束。
4. SAM 时空复杂度的理解与简要证明
这里,只说明 $tot\leq 2\operatorname{strlen}(s) - 1$。
很明显,每一次最多只会多 2 个结点。
查询也是线性,不用多说。
5. 结语
如果你还没有理解的话,请喷作者并发再评论。
希望能帮助到你。