数学基础杂论

本人由于以前看过一些书，对一些知识有一定的了解，所以这里只讲自己不懂的知识和例题。

对于基础的算法，可能也会有简略的讲解。

0. 前言

有以下内容：

1. 筛质数
2. 同余（扩欧）
3. 中国剩余定理
4. 矩阵乘法（快速幂）
5. 组合计数（加乘原理，Lucas，Catalan）

1. 筛质数

以前写过，就放在这里了。

我的筛质数的 Blog

2. 同余

解决形如 $ax\equiv 1\pmod b$ 或 $ax+by=1$ 不定方程的算法，为扩展欧几里得算法。

利用欧几里得算法，我们就可以计算不同的状态之间的转移。

具体直接看代码。

typedef long long ll;
ll ExGCD(ll a,ll b,ll &x,ll &y){
	ll d;
    if(b==0) x=1,y=0,d=a;
    else
    {
		d=ExGCD(b,a%b,y,x),y-=a/b*x;
	}
	return d;
}

T1：青蛙的约会

题目传送门 Luogu

题目传送门 AcWing

模板题。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;

void ExGCD(ll a,ll b,ll &x,ll &y,ll &d)
{
	if (!b)
	{
		x=1,y=0;d=a;
		return;
	}
	ExGCD(b,a%b,y,x,d);
	y-=a/b*x;
}

int main()
{
	ll x,y,m,n,l;
	scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&l);
	ll a=x-y,b=n-m;
	ll d,t;ExGCD(b,l,x,y,d);
	if (a%d) puts("Impossible");
	else{
		x*=a/d;
		ll t=abs(l/d);
		printf("%lld\n",(x%t+t)%t);
	}
	return 0;
}

T2：最幸运的数字

题目传送门 AcWing

首先，$x$ 个 8 可以表示为 $\dfrac89(10^x-1)$，那么 $L|\dfrac89(10^x-1)|\Leftrightarrow \dfrac{9L}d|\dfrac8d(10^x-1)$，其中 $\gcd(8,L)=d$。

又 $\dfrac8d$ 与左边互质，所以无需该数。

于是，我们令 $c=\dfrac{9L}d$，则变为 $10^x\equiv1\pmod c$。

首先，如果 $\gcd(10,c)\not=1$，那么原方程无解（因为左边一定是 $c$ 的倍数，而右边不是）。

又知道 $10^{\varphi(c)}\equiv1\pmod c$，于是 $\varphi(c)$ 满足答案。

那么，怎样求一个最小的呢？

证明： 最小的 $x$ 一定是 $\varphi(c)$ 的约数。

（以下模的方程省略 $\pmod c$）

使用反证法。

假设 $x\not|\varphi(c)$，那么可以写为 $\varphi(c)=qx+r$，其中 $0<r<x$。

首先，由于 $10^x\equiv1$，则 $10^{qx}\equiv1$。

又 $10^{\varphi(c)}\equiv1$，即 $10^{qx+r}\equiv1$。

所以，$10^r\equiv1$，与 $x$ 的最小性矛盾。

故原命题成立。

证毕。

回到本题，只需我们枚举约数即可。

详细代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
ll l;

ll qmul(ll a,ll b,ll p)//快速乘（可能爆 long long） 
{
    ll res=0;
    while (b)
    {
        if (b&1) res+=a,res%=p;
        b>>=1;a+=a;a%=p;
    }
    return res;
}

ll qpow(ll a,ll b,ll p)//快速幂 
{
    ll res=1;
    while (b)
    {
        if (b&1) res=qmul(res,a,p);
        b>>=1;a=qmul(a,a,p);
    }
    return res;
}

ll get_phi(ll n)
{
    ll res=n;
    for (ll i=2;i<=n/i;++i)
        if (n%i==0)
        {
            while (n%i==0) n/=i;
            res=res/i*(i-1);
        }
    if (n>1) res=res/n*(n-1);
    return res;
}

int main()
{
    int t=0;
    while ((~scanf("%d",&l))&&l)
    {
        ll d=1;
        while (l%(d*2)==0&&d*2<=8) d*=2;
        ll n=9*l/d;
        ll phi=get_phi(n);
        ll res=(1ll<<60);
        for (ll i=1;i<=phi/i&&i<=res;++i)
            if (phi%i==0)
            {
                if (qpow(10,i,n)==1) res=min(res,i);
                if (qpow(10,phi/i,n)==1) res=min(res,phi/i);
            }
        if (res==(1ll<<60)) res=0;
        printf("Case %d: %lld\n",++t,res);
    }
    return 0;
}

3. 中国剩余定理

巧了，我以前也写过。

我的中国剩余定理 Blog

4. 矩阵乘法

不想讲，主要是定义对于 OI 毫无用处。

自己去百度吧 （逃）。

只放一个代码。

详细代码

typedef long long ll;
const int N=202;
const ll INF=1e16;
const ll Mod=1e9+7;

class Matrix{
    public:
    ll a[205][205];
    int n,m;
    inline void clean(int _n,int _m)
    {
        n=_n,m=_m;
        for (int i=0;i<n;++i)
            for (int j=0;j<m;++j) a[i][j]=0;
    }
    Matrix operator *(const Matrix &b) const{
        Matrix c;
        if (m!=b.n) return c;
        c.clean(n,b.m);
        for (int i=0;i<c.n;++i)
            for (int j=0;j<c.m;++j)
                for (int k=0;k<m;++k) c.a[i][j]+=a[i][k]*b.a[k][j],c.a[i][j]%=Mod;
        return c;
    }
}F0;

Matrix operator ^(Matrix a,ll n)
{
    Matrix ans=a;n--;
    while (n)
    {
        if (n&1) ans=ans*a;
        a=a*a;
        n>>=1;
    }
    return ans;
}

在 OI 中，主要使用快速幂优化。

也就是上面的最后一个重载运算符。

T1：[HNOI2008]GT考试

题目传送门 Luogu

题目传送门 LOJ

可以利用矩阵快速幂优化。

组合计数

如果你小学（？）学过的话，就会觉得不太难。

方面特别多，我们一个一个看（以例题看）。

T1：牡牛和牝牛

题目传送门 LOJ

这个是一种组合计数。

用 $f(i)$ 表示所有以 $1$ 结尾的长度为 $i$ 的字符串的数量。

那么，我们可以得到：

$$f(i)=\sum_{j=0}^{i-k-1}f(j)$$

答案为：

$$ans=\sum_{i=0}^{n}f(i)$$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int N=5e5+10,Mod=5000011;
ll s[N],f[N];

int main()
{
	int n,k;cin>>n>>k;
	s[0]=1;
	for (int i=1;i<=n;++i)
	{
		f[i]=s[max(i-k-1,0)];
		s[i]=s[i-1]+f[i];s[i]%=Mod;
	}
	cout<<s[n]<<endl;
	return 0;
}

T2：车的放置

题目传送门 Luogu

题目传送门 LOJ

可以使用化整为零的思想。

分情况讨论，并将所有的答案加起来。

首先，我们考虑矩形求答案。

假设长为 $n$，宽为 $m$，那么，答案为：

$$ans=\binom mk*P_n^k$$

回归本题，枚举上面放 $i$ 个车，下面放 $k-i$ 个车。

注意，我们要首先计算上面的，因为上面的对下面的影响是固定的，而下面对上面的影响可能变化。

所以，答案为：

$$ans=\sum_{i=1}^{k}{\binom bi*P_a^i*\binom d{k-i}*P_ {a+c-i}^{k-i}}$$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int N=2010,Mod=1e5+3;

int a,b,c,d,k;
ll f[N],inv[N];

ll qpow(ll a,ll b)
{
	ll res=1;
	while (b)
	{
		if (b&1) res*=a,res%=Mod;
		a*=a;a%=Mod;b>>=1;
	}
	return res;
}

void init(int n)
{
	f[0]=inv[0]=1;
	f[1]=inv[1]=1;
	for (int i=2;i<=n;++i) f[i]=f[i-1]*i%Mod,inv[i]=qpow(f[i],Mod-2);
	return;
}

ll C(int n,int m)
{
	if (m>n) return 0;
	return f[n]*inv[n-m]%Mod*inv[m]%Mod;
}

ll P(int n,int m)
{
	if (m>n) return 0;
	return f[n]*inv[n-m]%Mod;
}

int main()
{
	cin>>a>>b>>c>>d>>k;
	init(N-1);
	ll res=0;
	for (int i=0;i<=k;++i)
		res+=C(b,i)*P(a,i)%Mod*C(d,k-i)%Mod*P(a+c-i,k-i)%Mod,res%=Mod;
	cout<<res<<endl;
	return 0;
}

T3：数三角形

题目传送门 Luogu

题目传送门 LOJ

我们可以使用容斥原理的思想。

首先，总方案为 $\binom {m*n}3$。

减去的就是三点共线的情况。

首先，水平的和竖直的情况共有 $n\binom m3+m\binom n3$。

然后，我们考虑斜率不为 0 的情况。

首先，对于每一个斜率小于 0 的情况，都可以转化为大于 0 的情况。

按照左下角的位置，划分为 $n*m$ 种情况。

对于每一个点 $(i,j)$ 再按照右上角的位置划分为 $(n-i)*(m-j)$ 种情况。

怎样求在上面的点的数量呢？

假设第二次选出的点为 $(x,y)$。

可以发现，就是 $\gcd(x-i,y-j)-1$ 种情况。

T4：序列统计

题目传送门 LOJ

首先，我们可以映射为 $[0,R-L]$ 的序列。

然后使用差分思想，设 $x_i=a_i-a_{i-1}$，那么原问题转化为 $x_1+x_2+…+x_k\leq R-L,x_i\geq 0$，其中 $k$ 为长度。

那么，令 $y_i=x_i+1$，那么变为 $y_1+y_2+…+y_k\leq R-L+k$。

假设 $y_{k+1}$ 为 $R-L+k+1-(y_1+y_2+…+y_k)$，则 $y_{k+1}\geq 1$，那么原式变为 $y_1+y_2+…+y_{k+1}=R-L+k+1$。

利用隔板法，就可以得到答案 $\binom {R-L+k}k$。

于是，总答案就为：

$$ans=\sum_{k=1}^{N}{\binom {R-L+k}k}=\sum_{k=1}^{N}{\binom {R-L+k}{R-L}}$$

又因为 $\binom ab=\binom{a-1}b+\binom{a-1}{b-1}$，于是：

$$ans=\binom{R-L+1}{R-L+1}+\sum_{k=1}^{N}{\binom {R-L+k}{R-L}}-1$$

利用公式，就可以得到：

$$ans=\binom{R-L+N+1}{R-L+1}-1$$

注意，这里一定要看懂，可能有些绕！

接下来，因为 $R,L,N\leq10^9$，所以要使用 Lucas。

Lucas 定理。

这个大概背代码就可以了。

核心就是 $\binom nm\equiv\binom{n\%p}{m\%p}* \binom{n/p}{m/p}\pmod p$，其中 $p$ 为质数。

int qpow(int a,int n,int p)
{
    int ans=1;
    while (n)
    {
        if (n&1) ans*=a,ans%=p;
        n>>=1;
        a*=a;a%=p;
    }
    return ans;
}

int cm(int a,int b,int p)
{
    int ans=1,tmp=1;
    for (int j=1,i=a;j<=b;--i,++j) ans*=i,ans%=p;
    for (int i=1;i<=b;++i) tmp*=i,tmp%=p;
    return ans*qpow(tmp,p-2,p)%p;
}

int lucas(int n,int m,int p)
{
    if (m==0) return 1;
    return lucas(n/p,m/p,p)*cm(n%p,m%p,p)%p;
}

就可以了！

详细代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int N=1e6+10;
const ll Mod=1e6+3;
int n,l,r;

ll qpow(ll a,ll b)
{
	ll res=1;
	while (b)
	{
		if (b&1) res*=a,res%=Mod;
		b>>=1;
		a*=a;a%=Mod;
	}
	return res;
}

ll C(int n,int m)
{
	ll ans=1,fac=1;
	for (int i=1;i<=m;++i) fac*=i,fac%=Mod;
	for (int i=n-m+1;i<=n;++i) ans*=i,ans%=Mod;
	return ans*qpow(fac,Mod-2)%Mod;
}

ll Lucas(ll n,ll m)
{
	if (n<Mod&&m<Mod) return C(n,m);
	return Lucas(n/Mod,m/Mod)*C(n%Mod,m%Mod)%Mod;
}

int main()
{
	int t;scanf("%d",&t);
	while (t--)
	{
		scanf("%d %d %d",&n,&l,&r);
		ll res=Lucas(r-l+n+1,r-l+1);
		printf("%lld\n",res?res-1:Mod-1);
	}
	return 0;
}

T5：网络

题目传送门 LOJ

Catalan。

假设我们从 (0,0) 走到 (n,n)，其中横坐标必须大于等于纵坐标，请问答案有多少种。

首先，总数即为 $\binom {2n} {n}$，因为我们要在 $2n$ 次里选出 $n$ 个向上。

利用容斥原理，我们发现 $ans=\binom {2n} n$ 再减去不合法的即可。

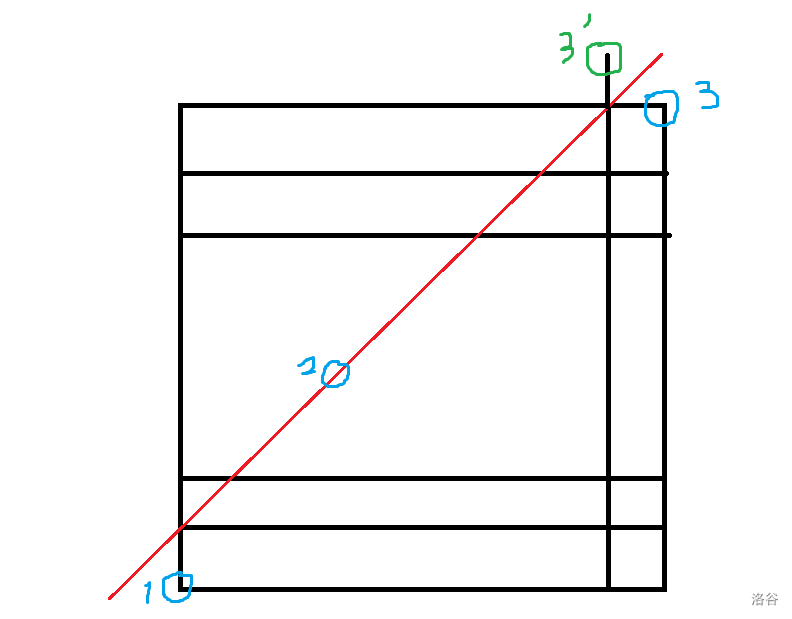
如果不合法，那么我们一定有一个 2 点，在红线上。

将 2 到 3 的路径沿红线翻转，那么，就得到一个 3‘ 点。

同理，我们可以将每一个到 3’ 点沿红线翻转到 3 点。

到 3’ 的方法有 $\binom{2n}{n+1}$ 种。

答案即为 $ans=\binom{2n}{n}-\binom{2n}{n+1}$。

回到本题，又有了一些变化。

我们可以使用类似的映射方式。

$n\not=m$，需要我们更改一下。

首先，将 $(n,m)$ 整体下移一格，得到 $(n,m-1)$，同时将红线向下平移一格，再关于红线对称，得到 $(m-1,n)$，再上移一格，最后得到 $(m-1,n+1)$。

所以，不合法的方案数即为 $\binom{m+n}{m-1}$。

答案即为 $ans=\binom{m+n}m-\binom{m+n}{m-1}$。

注意，本题答案很大，需要高精。

（写了一天）

详细代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long ll;
const int N = 1e4 + 10;
const int B = 1e4;
int prime[N], cnt;
bool st[N];
//支持正整数的加减乘除乘方，位数小于 40000
class num {
private:
    ll a[N];
    const ll B = 1e4;

    inline void adjust() {
        for (int i = 1; i <= a[0]; ++i)
            a[i + 1] += a[i] / B, a[i] %= B;

        while (a[a[0] + 1] > 0)
            a[0]++, a[a[0] + 1] += a[a[0]] / B, a[a[0]] %= B;

        while ((!a[a[0]]) && a[0] > 1)
            a[0]--;
    }
public:
    inline void init(int x) {
        memset(a, 0, sizeof a);
        a[0] = 1;
        a[1] = x % B;

        while (x >= B)
            a[++a[0]] = x / B, x /= B;
    }

    const num operator =(const num &b) {
        init(0);

        for (int i = 0; i <= b.a[0]; ++i)
            a[i] = b.a[i];

        return b;
    }

    const bool operator ==(const num &b)const {
        if (a[0] != b.a[0])
            return false;

        for (int i = 1; i <= a[0]; ++i)
            if (a[i] != b.a[i])
                return false;

        return true;
    }

    const bool operator <(const num &b)const {
        if (a[0] != b.a[0])
            return a[0] < b.a[0];

        for (int i = 1; i <= a[0]; ++i)
            if (a[i] != b.a[i])
                return a[i] < b.a[i];

        return false;
    }

    const bool operator <=(const num &b)const {
        if (a[0] != b.a[0])
            return a[0] < b.a[0];

        for (int i = 1; i <= a[0]; ++i)
            if (a[i] != b.a[i])
                return a[i] < b.a[i];

        return true;
    }

    const bool operator >(const num &b)const {
        if (a[0] != b.a[0])
            return a[0] > b.a[0];

        for (int i = 1; i <= a[0]; ++i)
            if (a[i] != b.a[i])
                return a[i] > b.a[i];

        return false;
    }

    const bool operator >=(const num &b)const {
        if (a[0] != b.a[0])
            return a[0] > b.a[0];

        for (int i = 1; i <= a[0]; ++i)
            if (a[i] != b.a[i])
                return a[i] > b.a[i];

        return true;
    }

    const num operator +(const num &b)const {
        num ans;
        ans.init(0);
        ans.a[0] = max(a[0], b.a[0]);

        for (int i = 1; i <= ans.a[0]; ++i)
            ans.a[i] = a[i] + b.a[i];

        ans.adjust();
        return ans;
    }

    const num operator -(const num &x)const {
        num ans;
        ans.init(0);
        ans.a[0] = a[0];
        num b = x;

        for (int i = 1; i <= a[0]; ++i)
            if (a[i] > b.a[i])
                ans.a[i] += a[i] - b.a[i];
            else
                ans.a[i] += a[i] + B - b.a[i], ans.a[i + 1]--;

        ans.adjust();
        return ans;
    }

    const num operator *(const num &b)const {
        num ans;
        ans.init(0);
        ans.a[0] = a[0] + b.a[0];

        for (int i = 1; i <= a[0]; ++i) {
            for (int j = 1; j <= b.a[0]; ++j)
                ans.a[i + j - 1] += a[i] * b.a[j];

            ans.adjust();
        }

        return ans;
    }

    const num operator *(const int &b)const {
        num ans=*this;
        int t=0;
        for (int i = 1; i <= a[0]; ++i)
            t+=a[i]*b,ans.a[i]=t%B,t/=B;
        while (t) ans.a[++ans.a[0]]=t%B,t/=B;
        return ans;
    }

    const num operator /(const int &b)const {
        num ans;

        for (int i = 0; i <= a[0]; ++i)
            ans.a[i] = a[i];

        int y = 0;

        for (int i = a[0]; i; --i)
            /*ans.a[i-1]+=a[i]%b*B,ans.a[i]/=b;*/
            y = B * y + ans.a[i], ans.a[i] = y / b, y %= b;

        ans.adjust();
        return ans;
    }

    const num operator ^(const int &x)const {
        if (!x) {
            num ans;
            ans.init(1);
            return ans;
        }

        num ans, now;

        for (int i = 0; i <= a[0]; ++i)
            now.a[i] = ans.a[i] = a[i];

        ll b = x - 1;

        while (b) {
            if (b & 1)
                ans = ans * now;

            now = now * now;
            b >>= 1;
        }

        return ans;
    };

    void print() {
        cout << a[a[0]];

        for (int i = a[0] - 1; i > 0; --i)
            printf("%lld%lld%lld%lld", a[i] / 1000, a[i] / 100 % 10, a[i] / 10 % 10, a[i] % 10);
    }
};

void init() {
    for (int i = 2; i < N; ++i) {
        // cout<<i<<endl;
        if (!st[i])
            prime[cnt++] = i;

        for (int j = 0; j < cnt && i * prime[j] < N; ++j) {
            st[i * prime[j]] = true;

            if (!(i % prime[j]))
                break;
        }
    }
}

ll get(ll n, ll p) {
    ll ans = 0;

    while (n)
        ans += n / p, n /= p;

    return ans;
}

num C(int n, int m) {
    num ans;
    ans.init(1);

    for (int i = 0; i < cnt; ++i) {
        int p = prime[i];

        if (p > n)
            return ans;

        ll tmp=1;
        ll t=get(n, p) - get(m, p) - get(n - m, p);
        /*if (p==2) printf("%d %d %d %d %d %d\n",get(n,p),get(m,p),get(n-m,p),n,m,n-m);
        printf("%d %d\n",p,t);*/
        while (t--) ans=ans*p;
    }

    return ans;
}

int main() {
    int n, m;
    cin >> n >> m;
    // puts("success");
    init();

    num res = C(n + m, m);
    res=res-C(n + m, n+1);
    res.print();
    return 0;
}

T6：[HNOI2009]有趣的数列

题目传送门 Luogu

题目传送门 LOJ

其实本题还是一个 Catalan。

怎样证明呢？

可以发现，

高斯消元

T1：球形空间生成器

题目传送门 Luogu

题目传送门 AcWing

根据球的性质，可以得到：

$$\begin{cases} (a_{1,1}-x_1)^2+(a_{1,2}-x_2)^2+...+(a_{1,n}-x_n)^2=R^2\\ (a_{2,1}-x_1)^2+(a_{2,2}-x_2)^2+...+(a_{2,n}-x_n)^2=R^2\\ ...\\ (a_{n+1,1}-x_1)^2+(a_{n+1,2}-x_2)^2+...+(a_{n+1,n}-x_n)^2=R^2 \end{cases}$$

是一个二次方程，其实不好解。

但是，我们可以相减，就可以把二次消掉了。

有些麻烦，懒得写公式了。

T2：开关问题

题目传送门 AcWing

本题是异或高斯消元法。

首先，发现：每一个开关最多开一次。

可以得到：影响该开关的所有开关的异或和再异或上初始的状态为终状态。

看代码就可以了。

容斥原理

T1：Devu 和鲜花

题目传送门 Luogu(RemoteJudge:Codeforces)

题目传送门 AcWing

首先，考虑每个盒子花有无限个。

那么，$x_1+x_2..+x_N=M(x_i\geq0)$，隔版法即可。

答案为 $\binom{N+M-1}{N-1}$。

然后考虑容斥原理。

首先，我们计算不满足第一个盒子的情况。

假设不满足第 $i$ 个盒子的情况为 $S_i$

利用容斥，我们可以得到

$$ans=\binom{M+N-1}{M-1}-\sum_{i=1}^{n}|S_i|+ \sum_{i=1}^{n}\sum_{j=i+1}^n|S_i\cup S_j|-...$$

可以将每一个理解为 $2^n$ 的二进制，每一位代表是否不满足该条件。

奇减偶加，就可以了。

Mobius 函数

（前面我开始没学懂）

定义 $\mu(x)$ 为莫比乌斯函数为：

$$\begin{array}{ll} 0(d_i>1)\\ -1(k\equiv1\pmod2)\\ 1(k\equiv0\pmod2) \end{array}$$

其中，$x=p_1^{d_1}p_2^{d_2}…p_k^{d_k}$，$p_i$ 为质数。

1. 求法

在线性筛上改进。

1. 如果是质数，那么 $\mu(x)=-1$。
2. 如果 $i\equiv0\pmod{prime[j]}$，那么说明有一个质数的次数超过 1，那么 $\mu(x)=0$
3. 否则，多了一个质数 $\mu(x)=-\mu(i)$。

for (int i=2;i<N;++i)
    {
        if (!st[i]) prime[cnt++]=i;
        for (int j=0;j<cnt&&prime[j]*i<N;++j)
        {
            st[i*prime[j]]=1;
            if (!(i%prime[j]))
            {
                mu[prime[j]*i]=0;
                break;
            }
            else mu[prime[j]*i]=-mu[i];
        }   
    }

2. 例题

T1：ZAP-queries/破译密码

题目传送门 Luogu

题目传送门 AcWing

首先，我们令 $f(x)$ 为满足 $\gcd(a,b)=x$ 的个数。

再定义 $F(X)$ 为 $x|\gcd(a,b)$ 的个数。

那么，根据莫比乌斯反演，可以得到：

$$F(x)=\sum_{x|k}f(k)=\lfloor\dfrac{a}{x}\rfloor\lfloor\dfrac{b}{x}\rfloor\\ f(x)=\sum_{x|k}\mu(\dfrac{k}{x})F(d)$$

线性筛可以求出 $\mu(x)$，于是 $O(n)$ 就可以求出了。

但是，本题有多组数据，还需要我们进一步优化。

我们发现，有一些相邻的 $F(d)$ 是相同的。

通过打表发现，每一段的最大值为 $n/(n/d)$，答案都为 $F(d)$。

就可以了。

详细代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int N=1e7+10;
int prime[N],cnt;
int mu[N],g[N],sum[N];
bool st[N];

void init()
{
    mu[1]=1;
    for (int i=2;i<N;++i)
    {
        if (!st[i]) mu[i]=-1,prime[cnt++]=i;
        for (int j=0;j<cnt&&i*prime[j]<N;++j)
        {
            st[i*prime[j]]=1;
            if (!(i%prime[j]))
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[i*prime[j]]=-mu[i];
        }
    }
    for (int j=0;j<cnt;++j)
        for (int i=1;i*prime[j]<N;++i)
            g[i*prime[j]]+=mu[i];
    for (int i=1;i<N;++i) sum[i]=sum[i-1]+g[i];
}

int main()
{
    init();
    int t,n,m;cin>>t;
    while (t--)
    {
        scanf("%d %d",&n,&m);
        if (n>m) swap(n,m);
        ll res=0;
        for (int l=1,r;l<=n;l=r+1)
        {
            r=min(n,min(n/(n/l),m/(m/l)));
            res+=(sum[r]-sum[l-1])*(ll)(n/l)*(m/l);
        }
        printf("%lld\n",res);
    }
    return 0;
}

数学期望

来看一个简单的例题：

T1：绿豆蛙的归宿

题目传送门 Luogu

题目传送门 AcWing

期望其实就是一个加权平均值。

详细代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=1e5+10,M=2e5+10;

int h[N],e[M],ne[M],w[M],idx;
int dout[N];
double f[N];

void add(int a,int b,int c)
{
    e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}

double dfs(int x)
{
    if (f[x]>=0) return f[x];
    f[x]=0;
    for (int i=h[x];~i;i=ne[i])
        f[x]+=(dfs(e[i])+w[i])/dout[x];
    return f[x];
}

int main()
{
    memset(h,-1,sizeof h);
    int n,m,a,b,c;cin>>n>>m;
    while (m--)
    {
        scanf("%d %d %d",&a,&b,&c);
        add(a,b,c);dout[a]++;
    }
    for (int i=1;i<=n;++i) f[i]=-1;
    printf("%.2lf\n",dfs(1));
    return 0;
}

T2：扑克牌

题目传送门 AcWing

记录 $f(a,b,c,d,x,y)$，前四个表示四种花牌的个数，后两个表示大小王分别放入的花色。

特别地，$x=4$ 表示大王未进入，$y=4$ 表示小王未进入。

直接递推即可。

详细代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;

const int N=14;
const double INF=1e8;

double f[N][N][N][N][5][5];
int ta,tb,tc,td;

bool check(int a,int b,int c,int d,int x,int y)
{
    if (a<ta) return 0;
    if (b<tb) return 0;
    if (c<tc) return 0;
    if (d<td) return 0;
    return 1;
}

double dp(int a,int b,int c,int d,int x,int y)
{
    int na=a+(x==0)+(y==0),
        nb=b+(x==1)+(y==1),
        nc=c+(x==2)+(y==2),
        nd=d+(x==3)+(y==3);
    double &v=f[a][b][c][d][x][y];
    if (check(na,nb,nc,nd,x,y)) return v=0;
    if (f[a][b][c][d][x][y]>=0) return f[a][b][c][d][x][y];
    int sum=a+b+c+d+(x!=4)+(y!=4);
    sum=54-sum;
    if (sum<=0) return v=INF;
    v=1;
    if (a<13) v+=(13.0-a)/sum*dp(a+1,b,c,d,x,y);
    if (b<13) v+=(13.0-b)/sum*dp(a,b+1,c,d,x,y);
    if (c<13) v+=(13.0-c)/sum*dp(a,b,c+1,d,x,y);
    if (d<13) v+=(13.0-d)/sum*dp(a,b,c,d+1,x,y);
    if (x==4)
    {
        double t=INF;
        for (int i=0;i<4;++i) t=min(t,dp(a,b,c,d,i,y));
        v+=1.0/sum*t;
    }
    if (y==4)
    {
        double t=INF;
        for (int i=0;i<4;++i) t=min(t,dp(a,b,c,d,x,i));
        v+=1.0/sum*t;
    }
    return v;
}

int main()
{
    cin>>ta>>tb>>tc>>td;
    memset(f,-1,sizeof f);
    dp(0,0,0,0,4,4);
    if (f[0][0][0][0][4][4]>INF/2) puts("-1.000");
    else printf("%.3lf\n",f[0][0][0][0][4][4]);
    return 0;
}