mydcwfy's Blog

斜率优化 DP

Posted on
Symbols count in article: 5.2k Reading time ≈ 11 mins.

DP 优化。

斜率优化 DP

1. 主要思想

斜率优化和单调队列、倍增、数据结构优化差不多，都是为了优化算法瓶颈的复杂度。

2. 方法

T1：任务安排

例题1：(Luogu)

例题1：(AcWing)

这题是斜率优化模板题的前身。

首先，我们发现启动一次，会对后面的所有都有影响。

所以，我们可以首先将该费用提前计算，为后面所有的费用乘上启动时间。

于是，我们较为简单地写出状态转移：

就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 2e5 + 10;
int n, sumt[N], sumc[N], f[N], S;

int main()
{
    memset(f, 0x3f, sizeof f);
    scanf("%d%d", &n, &S);
    for (int i = 1; i <= n; ++ i)
    {
        scanf("%d %d", &sumt[i], &sumc[i]);
        sumt[i] += sumt[i - 1];
        sumc[i] += sumc[i - 1]; 
    }
    f[0] = 0;
    for (int i = 1; i <= n; ++ i)
        for (int j = 0; j < i; ++ j)
            f[i] = min(f[i], f[j] + S * (sumc[n] - sumc[j]) + sumt[i] * (sumc[i] - sumc[j]));
    printf("%d\n", f[n]);
    return 0;
}

T2

题目传送门 LOJ

这个就是斜率优化最经典的题目了。

我们来看一下：

在求 $f[i]$ 的时候，可以认为 $i$ 相关的是常量，与 $j$ 相关的是变量。

所以，“参变分离”，可得：

将 $f[j]$ 看作 $y$，$sumc[j]$ 为 $x$，那么原式可以为：

那么，每一个决策都可以看作一个点，为 $(f[j],sumc[j])$。

我们现在想要 $f[i]$ 最小，即截距要最小。

然后，对于同一个 $i$ 来说，斜率是不变的。

那么，我们让斜率为 $S+sumt[i]$ 的一条直线一直向上移，当碰到第一个点时，就是最优决策了。

所以，对于每一个 $i$ 来说，都是这样来计算即可。

根据动态规划的优化根本原则，就是及时删除不需要的决策。

那些是不需要的决策呢？

首先，将所有点按横坐标排序（本题就是递增的）。

然后，将相邻两个点的斜率算出来。

注意，这里的斜率和上面的不同，定义是有区别的，务必分清！

以示区分，我在这里用横纵比表示这里的斜率（名字不好，凑合着用一下吧）

然后，如果相邻的纵横比是递减的，那么中间的点一定不会用到。

这个得到的图形就是凸包。

这里是难点，请务必理解。

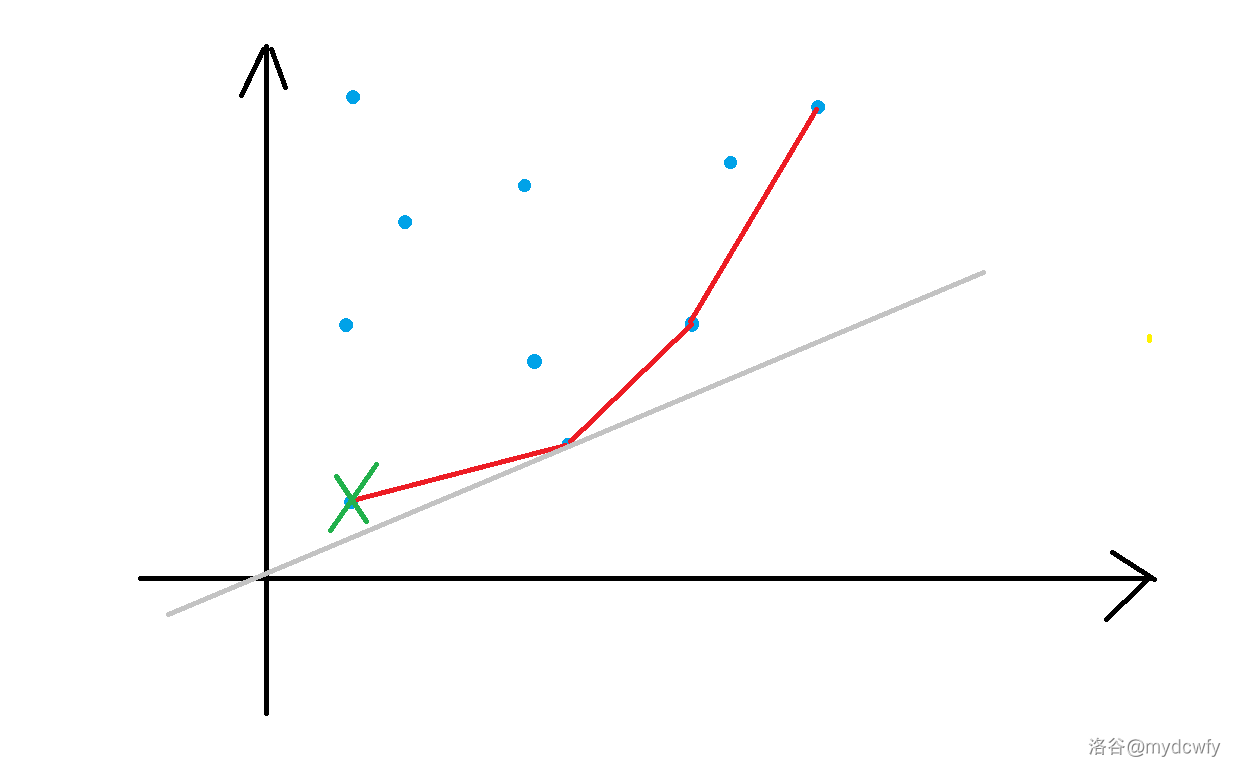
画个图。

然后，我们在凸包中找答案。

可以证明，答案一定是满足这样性质的点：他与前面点的横纵比小于斜率，与后面的点的纵横比大于斜率。

如果不理解的话，看一下上面的图就可以了。

于是，我们只要维护一个凸包即可，用平衡树维护即可，复杂度为 $O(n\log n)$。

其实，这也是 Graham 算法。

这个就是斜率优化的精髓。

然后，我们回归本题。

因为插入的点的横坐标一定是递增的，所以我们一定可以将点向后插入，就不需要平衡树了。

同时，因为本题查询的斜率也一定是递增的，所以如果有小于当前斜率的横纵比，直接就删除该点即可，就是上面被绿色叉掉的点。

在本题中，可以做到 $O(n)$，其他题可以优化到 $O(n\log n)$。

所有的题目，使用斜率优化时，都要弄清状态转移方程的 $y,x,k$ 再做。

代码不太长，但是细节有点多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;

typedef long long ll;
const int N = 3e5 + 10;
ll f[N], sumt[N], sumc[N];
int n, q[N], S;

int main()
{
    scanf("%d %d", &n, &S);

    for (int i = 1; i <= n; ++ i)
    {
        scanf("%lld %lld", &sumt[i], &sumc[i]);
        sumt[i] += sumt[i - 1];
        sumc[i] += sumc[i - 1];
    }

    int hh = 0, tt = 0;
    q[0] = 0;//f[j] = f[i] + (sumt[i] + S) * sumc[j] - sumc[n] * S - sumt[i] * sumc[i]

    for (int i = 1; i <= n; ++ i)
    {
        while (hh < tt && (f[q[hh + 1]] - f[q[hh]]) <= (sumt[i] + S) * (sumc[q[hh + 1]] - sumc[q[hh]]))
            hh ++;
        f[i] = f[q[hh]] - (sumt[i] + S) * sumc[q[hh]] + sumc[n] * S + sumt[i] * sumc[i];
        while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (sumc[i] - sumc[q[tt]]) <= 
        (f[i] - f[q[tt]]) * (sumc[q[tt]] - sumc[q[tt - 1]])) tt --;
        q[++ tt] = i;
    }

    printf("%lld\n", f[n]);

    return 0;
}

T3

题目传送门 Luogu

题目传送门 LOJ

这个就是刚才的题的加强版。

$T<0$，会发生什么呢？

看到上面的分析，我们发现就是斜率就不再具有单调性。

所以，我们不能删除横纵比小于当前斜率的点，于是就必须二分查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;

typedef long long ll;
const int N = 3e5 + 10;
ll sumt[N], sumc[N], f[N];
int S, q[N], n;

int main()
{
    scanf("%d %d", &n, &S);
    for (int i = 1; i <= n; ++ i)
    {
        scanf("%lld %lld", &sumt[i], &sumc[i]);
        sumt[i] += sumt[i - 1];
        sumc[i] += sumc[i - 1];
    }

    int hh = 0, tt = 0;

    for (int i = 1; i <= n; ++ i)
    {
        int l = hh, r = tt;
        while (l < r)
        {
            int mid = l + r >> 1;
            if ((f[q[mid + 1]] - f[q[mid]]) >= (sumt[i] + S) * (sumc[q[mid + 1]] - sumc[q[mid]]))
                r = mid;
            else l = mid + 1;
        }

        int j = q[r];
        f[i] = f[j] - (sumt[i] + S) * sumc[j] + S * sumc[n] + sumc[i] * sumt[i];

        while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (sumc[i] - sumc[q[tt]]) >=
        (f[i] - f[q[tt]]) * (sumc[q[tt]] - sumc[q[tt - 1]])) tt --;
        q[++ tt] = i;
    }

    printf("%lld\n", f[n]);

    return 0;
}

T4：运输小猫

题目传送门 AcWing

首先，我们求 $d_{1,i}$，即一个前缀和。

然后，假设 $S$ 为饲养员出发的时间。

那么，就可以得到 $S+d_i\geq t_i$，即 $S\geq t_i-d_i$。

令 $a_i=t_i-d_i$，那么每只小猫要求饲养员的出发时间的最大值。

再按照 $a_i$ 排序，于是就可以排成序列。

于是就转化为了一个较为经典的 DP 了。

设 $f[i,j]$ 为接走前 $i$ 只小猫用了 $j$ 个饲养员所需的最小等待时间。

用前缀和 $s_i$ 表示 $\sum_{j=1}^{i}a[i]$。

那么就可以得到：

接着，可以改写为：

就是一个斜率优化了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

typedef long long ll;
const int N = 1e5 + 10, P = 110;
ll d[N], a[N], f[P][N], s[N];
int n, m, p, q[N];

int main()
{
    scanf("%d %d %d", &n, &m, &p);
    for (int i = 2; i <= n; ++ i)
    {
        scanf("%d", &d[i]);
        d[i] += d[i - 1];
    }
    for (int i = 1, id; i <= m; ++ i)
    {
        scanf("%d %d", &id, &a[i]);
        a[i] -= d[id];
    }

    sort(a + 1, a + m + 1);
    for (int i = 1; i <= m; ++ i) s[i] = s[i - 1] + a[i];
    for (int j = 0; j <= p; ++ j)
        for (int i = 1; i <= m; ++ i) f[j][i] = 1ll << 60;
    for (int j = 1; j <= p; ++ j)
    {
        int hh = 0, tt = 0;
        q[0] = 0;
        for (int i = 1; i <= m; ++ i)
        {
            while (hh < tt && (f[j - 1][q[hh + 1]] + s[q[hh + 1]] - f[j - 1][q[hh]] - s[q[hh]])
            <= a[i] * (q[hh + 1] - q[hh]))
                hh ++;
            f[j][i] = f[j - 1][q[hh]] + a[i] * (i - q[hh]) - s[i] + s[q[hh]];
            while (hh < tt && (f[j - 1][q[tt]] + s[q[tt]] - f[j - 1][q[tt - 1]] - s[q[tt - 1]]) * (i - q[tt])
            >= (f[j - 1][i] + s[i] - f[j - 1][q[tt]] - s[q[tt]]) * (q[tt] - q[tt - 1]))
                tt --;
            q[++ tt] = i;
        }
    }
    
    ll res = 1ll << 60;
    for (int i = 1; i <= p; ++ i) res = min(res, f[i][m]);
    printf("%lld\n", res);

    return 0;
}