【CSP-S 2021 复习】图论总结

这里总结了一些以前没有写过的知识点（主要是因为知识点比较少，就不专门写了），同时对于考纲内的知识点，会附上一些自己的看法。可能有纰漏，望读者指出。

1. 大概内容

最短路
最小生成树与次小生成树
欧拉回路
Tarjan 与缩点，割点、桥
二分图
差分约束
拓扑排序
最近公共祖先与倍增

（一时想不起了，提高组考察似乎就这么多……

2. 详细内容

1）最短路

最短路估计是大家见过最多的图论了，因为这个算法虽然简单，但是变化莫测，难度几乎没有上限，甚至各种高级算法的基础是它（费用流等），还可以和各种题型进行结合，导致难度骤增。

关于算法，四种，不用多说：Floyd，Dijkstra，Bellman-Ford，SPFA。

考场上的选择：一般使用 Dijkstra，不要使用 SPFA（因为最坏复杂度太差，而且能被卡死，除非明摆着的 Dijkstra 过不了的时候，还能一些 ~~（满）~~ 分），多源求最短路用 Floyd，特殊情况用 Bellman-Ford。

前面三种的区分比较明显，因为时间复杂度不同，Dijkstra 是 $O(m\log n)$，SPFA 是 $O(km)$，Floyd 是 $O(n^3)$。

什么是 Bellman-Ford 的特殊情况呢？

比如这样一道题。

给定一张有向图，求对于每一个 $k\in[1,n-1]$，求源点 $1$ 到每一个点走不超过 $k$ 条边的最短路。为了了避免输出量极大，对于每一个 $k$，输出所有最短距离的异或和即可。无法到达的点设其最短距离为 $u\times1\times10^{14}$，$u$ 为其编号。$n\leq1000,m\leq5000,w_i\leq10^7$

这个就是一个经典的 Bellman-Ford 算法了。

const ll INF = 1e14;
struct Edge{
	int u, v, w;
}e[M];
ll d[N][N];
int n, m;

int main()
{
	for (int i = 1; i <= n; ++ i)
		for (int j = 0; j < n; ++ j) d[j][i] = INF;
	d[0][1] = 0;
	for (int k = 1; k < n; ++ k)
		for (int i = 1; i <= m; ++ i)
			if (d[k][e[i].v] > d[k - 1][e[i].u] + e[i].w) d[k][e[i].v] = d[k - 1][e[i].u] + e[i].w;
}

此外，感谢 @phigy 的建议，加上了最短路 DAG 的问题。

对于单源最短路来说，有一些边满足 $dis(i)=dis(j)+w(j,i)$，那么 $e(j,i)$ 就会在新图中，这就构成了最短路 DAG。

从 DAG 的源点开始走，任意走都是最短路——这个是比较特殊的性质。

void get_DAG(int st)
{
	Dijkstra(st);
	for (int x = 1; x <= n; ++ x)
		for (int i = h1[x]; ~i; i = ne[i])
			if (d[e[i]] == d[x] + w[i]) add(h2, x, e[i]);
}

比如这个题就是一个经典的题。

给定一张 $n$ 个点，$m$ 条边的有向图和起点 $S$，求$S$ 到每一个点最短路的路径条数。

这个直接在 DAG 上 bfs 就可以了。

还有一个：

给定一张 $n$ 个点，$m$ 条边的有向图和起点 $S$、终点 $T$，求 $S$ 到 $T$ 的最短路的必经边（即删除这条边后会导致最短路变大）。

比较难的解法是支配树，先求出 DAG 后，再求支配点。

但是一个偷懒的方法是：假设 $e(i,j)$ 满足 $count(S,i)*count(j,T)=count(S,T)$，其中 $count(i,j)$ 表示 $i$ 到 $j$ 的最短路径数。

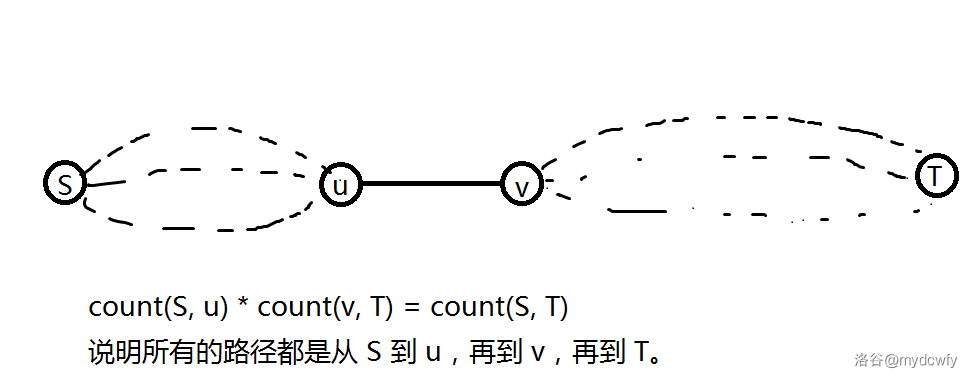
证明也很简单：如果两边的 $count$ 乘积等于总数的话，那么就不会存在其他路径了，也就是必经边了。

但是有可能爆 long long，所以使用 Hash。

2）最小生成树 & 次小生成树

最小生成树算法分别有 Kruskal($O(m\log n)/O(n\alpha(n))$)，Prim($O(n^2)$)，区别也很简单，稀疏图用 Kruskal，稠密图（用邻接矩阵存的）用 Prim。

推荐一个水题：P5994 [PA2014]Kuglarz

使用 Prim，时间复杂度为 $O(n^2)$。

同时一些题目本身是图，我们需要将其转化为一棵树，使答案可以很好计算。而转化为最小生成树是答案所求，所以我们先最小生成树。

注意，这里与最短路径 DAG 是有区别的，因为我们要根据不同的题目，具体选择需要的算法。

~~（这个找不到例题了……~~

次小生成树（严格）的模板题：P4180 [BJWC2010]严格次小生成树

这个是倍增的好题，我们马上再讲。（？

3）欧拉回路

博客讲得差不多了，我们就不啰嗦了，但是要强调的一个是：注意要先更新 $head$，然后再遍历，否则复杂度会假掉！

看一下最开始也是一般的代码：

void dfs(int x)
{
	for (int &i = h[x]; ~i; i = ne[i])
	{
		if (vis[i]) continue;
		vis[i] = 1;
		dfs(e[i]);
		ans[++ cnt] = i;
	}
}

int main()
{
	for (int i = cnt; i; -- i) cout << ans[i] << ' ';
}

注意，当我们 dfs(e[i]) 的时候，会导致我们当前的这个点的当前这一条边 $i$ 还没有被踢出 head[]，因为有回路导致重新遍历到这个点，可能会导致时间复杂度假掉。

正确的应该是这样：

void dfs(int x)
{
	for (int &i = h[x]; ~i;)
	{
		if (vis[i])
		{
			i = ne[i];
			continue;
		}
		vis[i] = 1;
		int j = e[i];
		i = ne[i];
		dfs(j);
		ans[++ cnt] = i;
	}
}

int main()
{
	for (int i = cnt; i; -- i) cout << ans[i] << ' ';
}

就避免了这种情况，

推荐一个题：P1127 词链

如果我们把这道题看作是哈密尔顿回路的话，那肯定就解不出来。

考虑将词语转化为边，然后将首尾字符变为点，就是欧拉回路了。

也涉及到了字符串，可能有一点麻烦。

4）Tarjan 缩点、各种双连通分量

这个真得不想再写博客了……

大概我那篇讲的挺清楚吗？

5）二分图

这个要注意染色法，最大匹配，Konig 定理，最大独立集几个知识点。

染色法其实是比较简单的，至少是 NOI 大纲-提高组区里的。

但是不代表其他的不考！

虽然考得比较少，但是不能说不可能。

匈牙利算法好打，一般不要使用 dinic 等（打错就尴尬了

6）差分约束

差分约束似乎不被重视，但是 2021 联合省选 D1T2 就考到了。

所以，还是要学习。

一般只能使用 SPFA（完全图除外），因为没法跑 Dijkstra。

还是要注意：最小值跑最长路，最大值跑最短路！

其他没什么说的了。

7）拓扑排序

这个比较简单了，只能在 DAG（有向无环图）上使用。

一般有 DAG DP 问题。

8）最近公共祖先

a. 暴力

选择深度较大的点向上跳，直到碰到为止。

时间复杂度为 $O(n)$。

int LCA(int x, int y)
{
	while (x != y)
	{
		if (dep[x] < dep[y]) swap(x, y);
		x = fa[x];
	}
	return x;
}

主要用在树的形态会发生改变的时候。

b. 倍增

考虑优化暴力。

我们可以预处理，对于每一个 $x$，$f[x][i]$ 表示 $x$ 的 $2^i$ 次跳过后走到的节点。

首先跳到同一深度。

然后 $i$ 从大向小枚举，如果跳到的位置不同，就可以跳。

这样的话，一定只剩一步就跳到相同的位置了。

时间复杂度为 $O(n\log n)-O(\log n)$

const int N = 1e5 + 10, L = 19;
int h[N], e[N << 1], ne[N << 1], idx;
int f[N][L + 1], dep[N];

void dfs(int x, int fa)
{
	f[x][0] = fa, dep[x] = dep[fa] + 1;
	for (int i = 1; i <= L; ++ i) f[x][i] = f[f[x][i - 1]][i - 1];
	for (int i = h[x]; ~i; i = ne[i])
		if (e[i] != fa) dfs(e[i], x);
}

int LCA(int x, int y)
{
	if (dep[x] < dep[y]) swap(x, y);
	for (int i = L; i >= 0; -- i)
		if (dep[f[x][i]] >= dep[y]) x = f[x][i];
	if (x == y) return x;//注意本身就相会的情况
	for (int i = L; i >= 0; -- i)
		if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
	return f[x][0];
}

~~大家应该都知道吧~~

c. Tarjan（跳过

d. ST 表

考虑 dfn 序（话说我在网上找了很久，dfn,euler,dfs 序各家说法不一，我也不太清楚

大致思路是：遍历到一个点的时候加在序列末尾，记当前位置为 $fi(x)$，然后它的一个子树走到另一个子树时，也要将 $x$ 加在序列末尾。

得到的序列可以证明不会超过 $2\times n-1$。

然后，我们找 $lca(x,y)$ 时，可以在序列里 $[fi(x), fi(y)]$ 中找到深度最小的点，一定就是答案。

为什么呢？原因很简单：因为 $[fi(x),fi(y)]$ 之间，一定会有 $lca$ 的出现，因为 $x,y$ 在 $lca$ 的不同子树，遍历不同子树的时候会记下 $lca$。

很明显，$lca$ 上面的 $fa(lca)$ 是不会在这之间的，因为 $x,y$ 是同一子树。

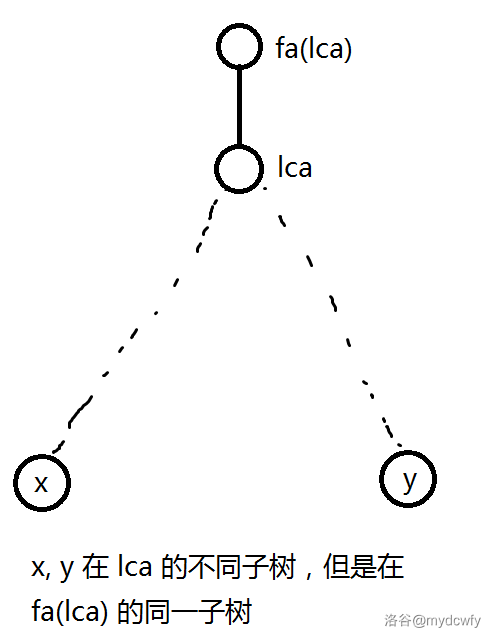
剩下的可以使用 ST 表维护了。

时间复杂度 $O(n\log n)-O(1)$

const int N = 1e5 + 10, L = 20;
int h[N], e[N << 1], ne[N << 1], idx;
int dep[N], st[N << 1][L], lg[N << 1], tot, fi[N];

int dep_min(int x, int y)
{
	return dep[x] < dep[y] ? x : y;
}

void dfs(int x, int fa)
{
	st[++ tot][0] = x, dep[x] = dep[fa] + 1, fi[x] = tot;
	for (int i = h[x]; ~i; i = ne[i])
		if (e[i] != fa) dfs(e[i], x), st[++ tot][0] = x;
}

void prework_st(){
	for (int i = 2; i <= tot; ++ i) lg[i] = lg[i >> 1] + 1;
	for (int j = 1; (1 << j) <= tot; ++ j)
		for (int i = 1; i + (1 << j) - 1 <= tot; ++ i)
			st[i][j] = dep_min(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}

int LCA(int x, int y)
{
	if (fi[x] > fi[y]) swap(x, y);
	int Lg = lg[fi[y] - fi[x] + 1];
	return dep_min(st[fi[x]][Lg], st[fi[y] - (1 << Lg) + 1][Lg]);
}

9）倍增

这个看似简单，我们拿两道题来看一下（前面的严格次小生成树在这里）。

T1：严格次小生成树

这个我们慢慢讲。

首先，我们跑一遍最小生成树，然后我们考虑再加入一条边，然后删除一条边。

很明显，假设一条边是 $e(u,v)$，我们应该删除 $u,v$ 路径上的一条边。

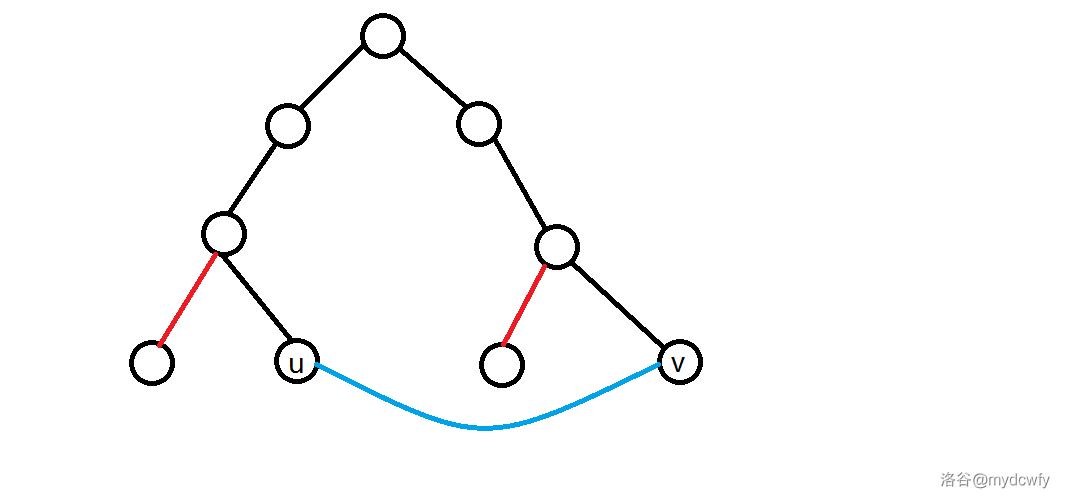
黑色的边就是我们可以删除的边，因为只有这些边中的一个被删除，原图仍然是树。

还可以得到一个结论：$\max_{e\in P(u,v)}(e.w)\leq w(u,v)$。（$P(u,v)$ 是指这条路径）

这个也显然，因为如果有边大于 $w(u,v)$ 的话，我们可以用 $w(u,v)$ 替换它，就答案更小了。

回到本题，我们删除哪条边呢？

明显应该删除 $P(u,v)$ 最大的边啊！（这样答案才最小

但是，得有一个前提：$\max_{e\in P(u,v)}(e.w)<w(u,v)$，否则就不是严格的了。

碰上 $=$ 怎么办呢？我们就删除次大边就是了。

那么，现在我们处理的问题就是怎样找到最大边和严格次大边。

倍增就可以解决这个问题了。

$g[x][i][0]$ 表示 $x$ 向上跳 $2^i$ 所经历的边的最大值，$g[x][i][1]$ 为严格次大值。

回顾 $\text{LCA}(x,y)$ 的算法，我们就可以处理了。

void dfs(int x, int fa)//预处理
{
    for (int i=1;i<=L;++i)
    {
        f[x][i]=f[f[x][i-1]][i-1];
        g[0][x][i]=max(g[0][f[x][i-1]][i-1],g[0][x][i-1]);
        if (g[0][x][i-1]<g[0][f[x][i-1]][i-1])
        {
            g[1][x][i]=max(g[0][x][i-1],g[1][f[x][i-1]][i-1]);
        }
        else if (g[0][x][i-1]==g[0][f[x][i-1]][i-1])
        {
            g[1][x][i]=max(g[1][x][i-1],g[1][f[x][i-1]][i-1]);
        }
        else
        {
            g[1][x][i]=max(g[1][x][i-1],g[0][f[x][i-1]][i-1]);
        }
    }
}

int lca(int x,int y,int now)//now 是指加入的边，不能与之相同
{
    if (d[x]<d[y]) swap(x,y);
    int ans=-INF;
    for (int i=L;i>=0;--i)
        if (d[f[x][i]]>=d[y])
        {
            if (g[0][x][i]==now) ans=max(ans,g[1][x][i]);
            else ans=max(ans,g[0][x][i]);
            x=f[x][i];
        }
//  cout<<x<<' '<<y<<endl;
    if (x==y) return ans;
    for (int i=L;i>=0;--i)
        if (f[x][i]!=f[y][i])
        {
            if (g[0][x][i]==now) ans=max(ans,g[1][x][i]);
            else ans=max(ans,g[0][x][i]);
            if (g[0][y][i]==now) ans=max(ans,g[1][y][i]);
            else ans=max(ans,g[0][y][i]);
            x=f[x][i];y=f[y][i];
        }
    int i=0;
    if (g[0][x][i]==now) ans=max(ans,g[1][x][i]);
    else ans=max(ans,g[0][x][i]);
    if (g[0][y][i]==now) ans=max(ans,g[1][y][i]);
    else ans=max(ans,g[0][y][i]);
    return ans;
}

T2：跑路

这个题其实是比较简单的倍增题目。

因为这里明显在提示 $2^k$，所以我们考虑倍增求一次能达到的点。

$a[bit][i][j]$ 表示经过 $2^{bit}$ 次边，$i,j$ 是否互达。

这个可以使用 Floyd，$a[bit][i][j]|=a[bit-1][i][k]\odot a[bit-1][k][j]$。

对于 $d(i,j)$，$\exists bit\in[0,30],a[bit][i][j]=1$，则 $d(i,j)=1$。

然后 Floyd 跑就可以了。

for (int bit = 0; bit < 31; ++ bit)
    for (int k = 1; k <= n; ++ k)
        for (int i = 1; i <= n; ++ i)
            for (int j = 1; j <= n; ++ j)
                a[bit + 1][i][j] |= a[bit][i][k] & a[bit][k][j];

T3：电阻网络

~~（作为习题了吧~~

首先是可以分治的，然后对于并联电路，求最早交点。

可以倍增找交点，有点像 LCA。

这个不具体讲了。