KMP algorithm

比较简单的前置知识。

KMP

1. 所解决的问题

匹配一个字符串 $s[]$ 与模式字符串 $p[]$，计算有哪些点 $s[]$ 结尾的字符串与模式串（或前缀）完全相同。

通俗地讲，就是 $s[]$ 每一个起点（或终点）开始的字符串与 $p[]$ 前面相同的长度。

朴素算法是枚举起点（或终点），发现匹配即可。

枚举起点，一直匹配直到不相同为止。

2. 优化（核心思想）

定义 $next[i]$ 为以 i 结尾的模式串的前缀与后缀的相同最大长度（非自己）。

（ 大雾 ）

我们仔细想一想这句话，这句话是什么意思？

自己画个图，可以发现，当与字符串匹配时，如果当前匹配失败的话，我们需要倒退一定距离。

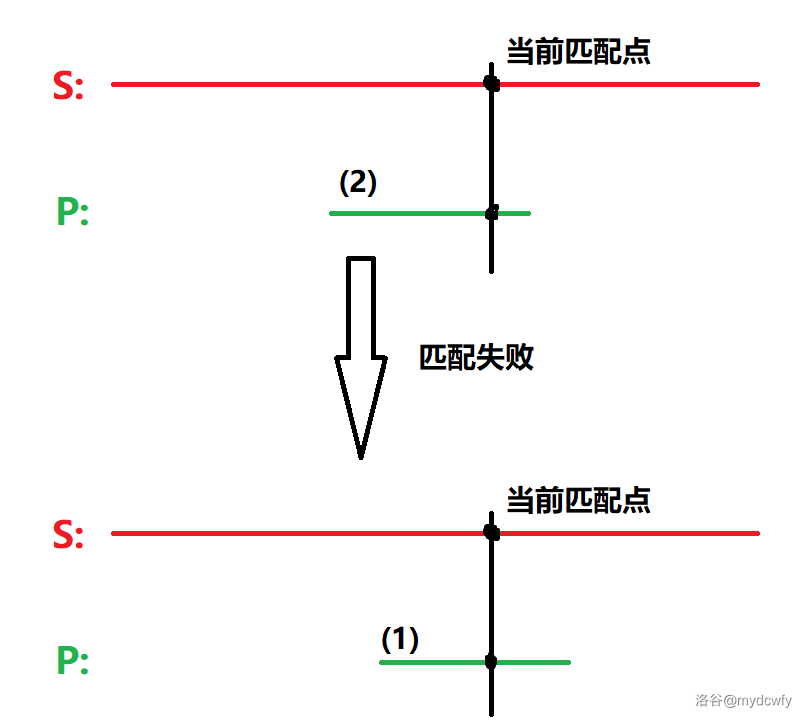
为了使之继续匹配（而不是从头开始），我们需要当前的后缀要与原来的前缀相同，就可以继续尝试匹配。

也就是 (2) 处的后缀和 (1) 处相同。

但又因为 (1) 是 (2) 的前缀。

所以，我们要预处理当前的前缀和后缀相同的最大距离。

这个的最大距离，就是 $next[i]$。

这是 KMP 的核心，请务必理解。

怎样求 next 数组呢？

其实，求 next 数组时，就是自己与自己匹配的过程。

s[] 和 p[] 的匹配就是寻找 s[i] 的后缀和 p[] 的前缀的匹配的最大距离。

将 s[] 也换成 p[]，就是自我匹配。

上代码。

for (int i=2,j=0;i<=len;++i)
{
	while (j!=0&&p[j+1]!=p[i]) j=ne[j];
	if (p[j+1]==p[i]) j++;
	ne[i]=j;
}

如果要匹配的话，照搬上面的即可，但注意如果匹配的话，要倒退一步，防止重复匹配。

for (int i=2,j=0;i<=n;++i)
{
	while (j&&s[i]!=p[j+1]) j=ne[j];
	if (p[j+1]==s[i]) j++;
	if (j==m) j=ne[j];
}