mydcwfy's Blog

线段树

Posted on
Symbols count in article: 9.9k Reading time ≈ 22 mins.

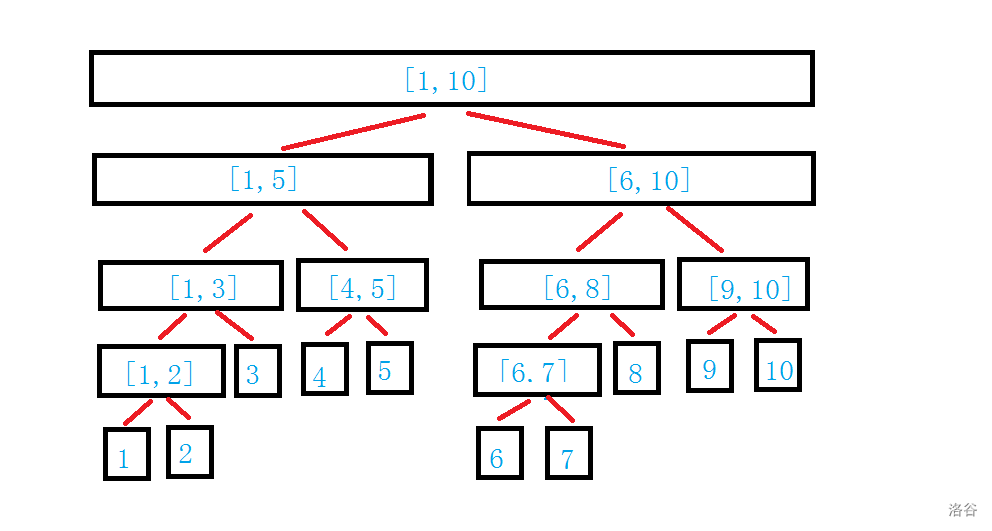
非常重要的数据结构

线段树

1.基本操作

pushup 和 pushdown

代码实现，有以下 5 种操作：

  1. $\operatorname{pushup}(u)$

  2. $\operatorname{build}(u,l,r)$

  3. $\operatorname{modify}(u,x,val)$ or $\operatorname{modify}(l,r,u,val)$（改为某一个值或加上某一个值）

  4. $\operatorname{query}(u,l,r)$

  5. $\operatorname{pushdown}(u,l,r)$

2.基本构造

对于每一个节点，都代表一个区间，该节点如果不是叶节点（即区间只有一个数），都会从中间断开，左右的区间的节点。

大多数情况，一个节点的父节点和子节点分别为 $[x/2]$ 和 $x \times 2$、$x\times 2 + 1$

可以发现，该树是完全二叉树。

由于最后一层不满，所以空间开为 $4\times n$。

一颗线段树

3.每个操作的具体实现

1）query

现在讲 query。

当遇到 $\operatorname{query}(u,l,r)$ 时，有下列二种情况：

$[l,r]\subseteq [T_l,T_r]$，直接返回。

$[l,r]\cap [T_l,T_r] \not= \emptyset$，递归有的区间。

注意，不可能出现无交集的情况，因为根本不会进入。

看似简单并且复杂度高，其实复杂度仅为 $O(\log n)$。一般为 $O(4\times \log n)$。

证明略，请读者自行分类证明。

2） modify

先讲单点。

比较简单，直接观察哪一边包含该点，进入即可。

再讲区间修改，即 $\operatorname{pushdown}(p,l,r)$。

3）pushdown

现在我们要区间修改。

与该区间有交集的节点最多有 $n$ 个，所以单次复杂度最坏为 $O(n)$。

所以有了 $lazytag$。

来自于 query，即完全包含时，就直接返回。

$lazytag$ 就记录当前对于整个区间的加，然后就不用继续向下递归。

注意，一般为了防止错误，一般该节点先加，到时候直接加儿子即可。

通过证明 query 的复杂度，可以发现 pushdown 整个复杂度为 $O(4\log n)$。

于是，在 query 时，如果需要递归该子区间时，直接将标记下传即可。

所以，此时就可以不需要记录 $lazytag$ 了。

以和为例：

最后清空当前节点的 $lazytag$ 即可。

4.例题

T1：[JSOI2008] 最大数

题目传送门 Luogu

题目传送门 ACWing

将动态改为静态。

先将插入加入序列，每一次真正插入时，就相当于单点修改。

就变成了模板题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define p1 p<<1
#define p2 p<<1|1
using namespace std;

const int N=2e5+10,INF=0x3f3f3f3f;

struct Segment
{
    int l,r,val;
}tr[4*N];

void build(int p,int l,int r)
{
    tr[p]=(Segment){l,r,0};
    if (l==r) return;
    int mid=l+r>>1;
    build(p1,l,mid);
    build(p2,mid+1,r);
}

void pushup(int p)
{
    tr[p].val=max(tr[p1].val,tr[p2].val);
}

void modify(int p,int x,int val)
{
    int l=tr[p].l,r=tr[p].r;
    if (l==r) 
    {
        tr[p].val=val;
        return ;
    }
    int mid=(l+r)>>1;
    if (x<=mid) modify(p1,x,val);
    else modify(p2,x,val);
    pushup(p);
}

int query(int p,int l,int r)
{
    if (tr[p].l>=l&&tr[p].r<=r) return tr[p].val;
    int mid=tr[p].l+tr[p].r>>1, ans=-INF;
    if (l<=mid) ans=max(ans,query(p1,l,r));
    if (r>mid) ans=max(ans,query(p2,l,r));
    return ans;
}

int main()
{
    char op[2];
    int m,p,last=0,x,n=0;
    scanf("%d %d",&m,&p);
    build(1,1,m);
    while (m--)
    {
        scanf("%s%d",op,&x);
        if (op[0]=='A')
        {
            x=(x+last)%p;
            modify(1,++n,x);
        }
        else
        {
            last=query(1,n-x+1,n);
            printf("%d\n",last);
        }
        
    }
    return 0;
}

T2:最大子段和

考虑在一个节点维护哪些信息。

首先要维护 $tmax$（该区间的最大子段和）。

考虑怎样从儿子转移到父亲。

可以发现，有可能跨越两个区间，即儿子的最大前缀和最大后缀。

易得 $tmax[u]=\max(tmax[l],tmax[r], rmax[l]+lmax[r])$。

但是我们也要维护 $lmax[u]$ 和 $rmax[u]$。

易得：$lmax[u]=max(lmax[l],sum[l]+lmax[r])$。

右边同理。

也要维护 $sum$。

至此得到解决。

T3：最大公约数

题目传送门 AcWing

一共有 2 个操作：区间加和求最大公约数。

考虑需要存的信息：

最大公约数。

但是，由于 $(a,b,c)$ 与 $(a+x,b+x,c+x)$ 没有直接关系，所以不好维护。

但是，如果只修改一个数，那么就很简单。（直接跟新即可）

将区间加改为单点加，直接差分即可。

又由辗转相除法的扩展，可得：

$(a[1],a[2]…,a[n])=(a[1],a[2]-a[1] … ,a[n]-a[n-1])$

证明：

先证 $d=(a[1],a[2],…,a[n])|(a[1],a[2]-a[1],…, a[n]-a[n-1])$

易得，$d|a[1],d|a[2]…$，所以 $d|a[2]-a[1]$。同理，就可以证明。

再证$d=(a[1],a[2]-a[1],…, a[n]-a[n-1])|(a[1],a[2],…,a[n])$

易得，$d|a[1],d|(a[2]-a[1])$，所以 $d|(a[2]-a[1]+a[1])$，同理可证。

证毕。

又因为 $\operatorname{gcd}(a,b,…)$ 具有交换性与结合性，所以可以分开求。

让线段树维护差分后的值，并在每一个节点维护最大公约数。

对于每一个询问，都要维护原区间第一个点的值，否则会出问题。

可以使用树状数组维护前缀和，也可以直接和线段树一起维护。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#define int long long
#define lowbit(x) (x & -x)
#define l(x) (x << 1)
#define r(x) (x << 1 | 1)
using namespace std;

typedef long long ll;
const int N = 5e5 + 10;
int n, m;
ll a[N];

class BIT{
private:
    ll tr[N];
public:
    void add(int x, ll c)
    {
        for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
    }
    ll query(int x)
    {
        ll res = 0;
        for (int i = x; i; i -= lowbit(i)) res += tr[i];
        return res;
    }
}bt;

struct Node{
    int l, r;
    ll val;
}tr[N << 2];

ll Gcd(ll a, ll b){return b ? Gcd(b, a % b) : a;}

void pushup(int x)
{
    tr[x].val = Gcd(tr[l(x)].val, tr[r(x)].val);
}

void build(int x, int l, int r)
{
    tr[x] = {l, r, a[l]};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(l(x), l, mid);
    build(r(x), mid + 1, r);
    pushup(x);
}

void modify(int x, int pos, ll c)
{
    if (tr[x].r < pos) return;
    if (tr[x].l == tr[x].r)
    {
        tr[x].val += c;
        return;
    }
    int mid = (tr[x].l + tr[x].r) >> 1;
    if (pos <= mid) modify(l(x), pos, c);
    else modify(r(x), pos, c);
    pushup(x);
}

int query(int x, int l, int r)
{
    if (l > r) return 0;
    if (tr[x].l >= l && tr[x].r <= r) return tr[x].val;
    int mid = (tr[x].l + tr[x].r) >> 1;
    if (r <= mid) return query(l(x), l, r);
    if (l > mid) return query(r(x), l, r);
    return Gcd(query(l(x), l, r), query(r(x), l, r));
}

main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) scanf("%lld", &a[i]);
    for (int i = n; i > 1; -- i) a[i] -= a[i - 1];
    for (int i = 1; i <= n; ++ i) bt.add(i, a[i]);
    build(1, 1, n);
    int l, r;
    ll d;
    char op[3];
    while (m --)
    {
        scanf("%s %d %d", op + 1, &l, &r);
        if (op[1] == 'Q') printf("%lld\n", abs(Gcd(bt.query(l), query(1, l + 1, r))));
        else{
            scanf("%lld", &d);
            modify(1, l, d), modify(1, r + 1, -d);
            bt.add(l, d), bt.add(r + 1, -d);
        }
    }
    return 0;
}

T4：一个简单的整数问题2/【模板】线段树1

题目传送门 Luogu

题目传送门 AcWing

上一次，我们使用了树状数组解决了本题。

这次，我们把他当做线段树的模板题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#define p1 p<<1
#define p2 p<<1|1
#define ll long long
using namespace std;

const int N=2e5+10;
struct Node{
    int l,r;
    ll sum,add;
}tr[4*N];

int a[N],n;

void pushup(int p)
{
    tr[p].sum=tr[p1].sum+tr[p2].sum;
}

void pushdown(int p)
{
    Node &root=tr[p],&left=tr[p1],&right=tr[p2];
    if (root.add==0) return ;
    left.add+=root.add,right.add+=root.add;
    left.sum+=root.add*(left.r-left.l+1),right.sum+=root.add*(right.r-right.l+1);
    root.add=0;
}

void build(int p,int l,int r)
{
    tr[p].l=l,tr[p].r=r;
    if (l==r) tr[p].sum=(ll)a[l],tr[p].add=0;
    else{
        int mid=l+r>>1;
        build(p1,l,mid);
        build(p2,mid+1,r);
        pushup(p);
    }
}

void modify(int p,int l,int r,int x)
{
    if (tr[p].l>=l&&tr[p].r<=r)
    {
        tr[p].sum+=(ll)(tr[p].r-tr[p].l+1)*x;
        tr[p].add+=(ll)x;
        return;
    }
    pushdown(p);
    int mid=tr[p].l+tr[p].r>>1;
    if (l<=mid) modify(p1,l,r,x);
    if (r>mid) modify(p2,l,r,x);
    pushup(p);
}

ll query(int p,int l,int r)
{
    if (tr[p].l>=l&&tr[p].r<=r) return tr[p].sum;
    pushdown(p);
    int mid=tr[p].l+tr[p].r>>1;
    ll sum=0;
    if (l<=mid) sum+=query(p1,l,r);
    if (r>mid) sum+=query(p2,l,r);
    return sum;
}

int main()
{
    int m;
    cin>>n>>m;
    for (int i=1;i<=n;++i) scanf("%d",a+i);
    build(1,1,n);
    char op[5];int l,r;
    ll x;
    while (m--)
    {
        scanf("%s%d%d",op,&l,&r);
        if (op[0]=='1') scanf("%lld",&x),modify(1,l,r,x);
        else printf("%lld\n",query(1,l,r));
    }
    return 0;
}

T5:亚特兰蒂斯

题目传送门 AcWing

这道题，我们讲另外一个线段树的重要应用：扫描线

扫描线的实质就是离散化加线段树（ 洛谷的标签 ）。

借助了积分的思想（不要被吓到了）。

将所有的 x 坐标离散化。

对于每一个相邻的 x 坐标，都有一些被覆盖，而且不是部分覆盖（即 x 坐标是被完全覆盖的，但 y 不一定）。

假设每个区间在 y 坐标上覆盖的长度为 $h[i]$，则答案为

考虑如何求 $h[i]$。

再次利用差分的思想，将整个矩形覆盖就相当于左边的线段所覆盖的 y 坐标加 1，右边的线段覆盖的 y 坐标减 1。

也就是每一个点被覆盖的次数，如果不为 0，就算上该节 点。

原题目转化为，怎样计算在同一线段上，被覆盖的长度。

所以，将纵坐标再维护成线段树。

又因为是差分思想，所以直接计算前缀和即可吗，每计算一条边就加入当前的线段树。

维护以下信息：

  • $cnt$ 记录当前区间的覆盖次数。

  • $len$ 不考虑当前节点的情况下，$cnt>0$ 的区间长度。

再根据它的特殊性质：在 query 的时候，只询问根节点，那么 query 一定不会使用 pushdown。

如果在 modify 时也不用使用 pushdown，那么就不需要 $lazytag$。

考虑该问题的特殊性质，对于同一区间，一定会先加一次，在减一次。

并且当前的节点，无论是多少，只要$x\geq 1$，就不会影响答案。

如果当前节点减完有为 0，就根据两个儿子的正确信息，就一定能维护当前节点的正确信息（儿子中没有被更改，是正确的）。

如果是加法，因为只会查询根节点，就不会用到儿子节点，所以无需管 psushdown。

并且，只要加大于 0 的节点，就不会影响答案。

如果等于 0 , pushdown 就不会执行。

这个题目的做法十分特殊，所以特意讲出来。

但是没有结束（ 雾 ）。

记得开头的标签吗？

我们还应该首先离散化，预处理相邻的距离。

还有一个细节，就是因为维护的是区间，所以应该是 $x[l]-x[r-1]$。

上代码（因为没有 $lazytag$，所以代码较短）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<vector>
#define l(p) (p<<1)
#define r(p) (p<<1|1)
using namespace std;

const int N=1e5+5;

struct Seg{
    double x,l,r;
    int k;
    const bool operator <(const Seg &e) const{
        return x<e.x;
    }
}seg[2*N];

struct Node{
    int l,r;
    double len;
    int cnt;
}tr[N<<3];

int n,m;

vector <double> t;

void pushup(int p)
{
    if (tr[p].cnt)
    {
        tr[p].len=t[tr[p].r+1]-t[tr[p].l];
        return;
    }
    if (tr[p].l==tr[p].r)
    {
        tr[p].len=0;
        return ;
    }
    tr[p].len=tr[l(p)].len+tr[r(p)].len;
}

void build(int p,int l,int r)
{
    tr[p]=(Node){l,r,0,0};
    if (l==r) return;
    int mid=l+r>>1;
    build(l(p),l,mid);
    build(r(p),mid+1,r);
    pushup(p);
}

void modify(int p,int l,int r,int k)
{
    // printf("%d %d %d %d %d\n",p,tr[p].l,tr[p].r,l,r);
    if (tr[p].l>=l&&tr[p].r<=r)
    {
        tr[p].cnt+=k;
        pushup(p);
        return;
    }
    int mid=tr[p].l+tr[p].r>>1;
    if (l<=mid) modify(l(p),l,r,k);
    if (r>mid) modify(r(p),l,r,k);
    pushup(p);
}

int find(int x)
{
    return lower_bound(t.begin(),t.end(),x)-t.begin();
}

int main()
{
    int T=0;
    while (scanf("%d",&n),n)
    {
        t.clear();double a,b,c,d;
        if (n==1)
        {
            scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
            printf("Test case #%d\n",++T);
            printf("Total explored area: %.2lf\n\n",(c-a)*(d-b));
            continue;
        }
        
        for (int i=1,j=0;i<=n;++i)
        {
            cin>>a>>b>>c>>d;
            seg[j++]=(Seg){a,b,d,1};
            seg[j++]=(Seg){c,b,d,-1};
            t.push_back(b);t.push_back(d);
        }
        sort(t.begin(),t.end());
        t.erase(unique(t.begin(),t.end()),t.end());
        if (t.size()==1)
        {
            printf("Test case #%d\n",++T);
            printf("Total explored area: 0.00\n\n");
        }
        build(1,0,t.size()-2);
        sort(seg,seg+2*n);
        double ans=0;
        for (int i=0;i<2*n;++i)
        {
            if (i>0) ans+=tr[1].len*(seg[i].x-seg[i-1].x);
            modify(1,find(seg[i].l),find(seg[i].r)-1,seg[i].k);
        }
        printf("Test case #%d\n",++T);
        printf("Total explored area: %.2lf\n\n",ans);
    }
    return 0;
}