Manacher

其实应用范围并不是很广。主要是预处理比较麻烦，而且很多问题回归原串的话是比较麻烦的。

1. 思想

解决最长回文串的问题。

其实字符串的思想其实是比较类似的，都是将一个 $O(n ^ 2)$ 或者更高的复杂度的一个算法降一个 $n$。

比如，这里的 Manacher，暴力匹配是 $O(n ^ 2)$，但是我们通过 Manacher，可以优化到 $O(n)$。（但是有二分加 Hash $O(n \log n)$）

2. 算法流程

1）预处理

由于 Manacher 比较拙劣只能处理长度为奇数的回文串，所以我们需要一些预处理。

其实很简单，我们直接在每两个字符之间加上另外一个没有出现过的字符，然后回文中心其实就是新加入的字符。

比如说，$\texttt{abba}$，然后我们变为：$\texttt{a|b|b|a}$，于是回文中心就是中间的 |。

注意我们可能会一些比较神奇的匹配出现，同时为了防止边界问题，我们在前面再加一个都没有出现过的字符。

于是就是：$\texttt{+a|b|b|a}$，很明显匹配的时候，我们会匹配到 + 的时候是一定不会在往前匹配的。所以一定不会导越界。

（代码中加的字符似乎不一样）

int readstr()//读入该串并转化
{
    int len = 0;
    str[++ len] = '@';
    str[++ len] = '%';
    char c;
    while ((c = getchar()) < 'a' || c > 'z');
    str[++ len] = c, str[++ len] = '%';
    while ((c = getchar()) >= 'a' && c <= 'z')
        str[++ len] = c, str[++ len] = '%';
    return len;
}

2）主流程

定义 $p(i)$ 表示以 $s(i)$ 为中心的最长回文串半径。比如 $\texttt{a|b|a}$，中间 $b$ 的下标是 $3$，那么 $p(3) = 3$，因为半径就是 $\texttt{b|a}$ 的长度。

首先，我们定义当前匹配的回文串最远可以达到 $r$，贡献这一个最远的是 $mid$，即 $r = \max(i + p(i) - 1)$，且 $r = mid + p(mid) - 1$。

我们计算 $p(i)$ 的时候，如果 $i < r$，那么就可以得到 $p(i)\geq \min(r - i + 1, p(2 * mid - i))$。为什么呢？

首先，我们计算 $p(i)$ 的时候，$mid < i$，然后 $2 mid - i < i$，所以 $p(i)$ 的信息可以由 $p(2 mid - i)$ 求出来。注意不能越出最长的回文串，不然就可能不是合法的。

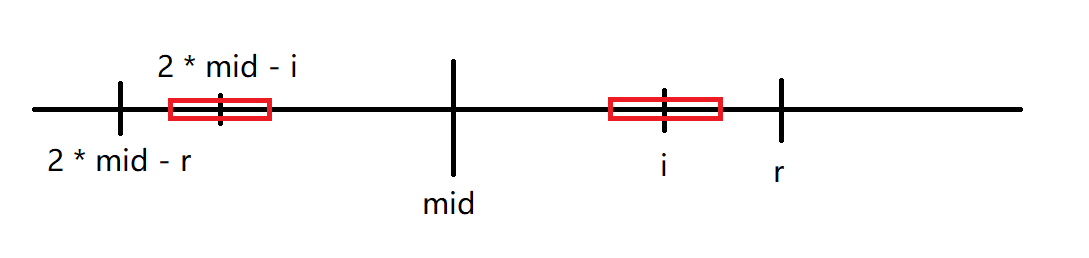
计算出来之后，我们直接暴力匹配就可以了。可以证明时间复杂度为 $O(n)$。先看代码。然后我们再证明复杂度。

如果要求原串的最长回文串，我们发现，不管是长度为奇数还是偶数，都是 $p(i) - 1$。看两个例子就可以了：$\texttt{|b|b|}$：$p(i) = 3$；$\texttt{|a|b|a|}$：$p(i) = 4$。

void Manacher()
{
    ans = -1;
    int ri = 1, mid = 1;
    for (int i = 1; i <= n; ++ i)
    {
        if (i < ri) p[i] = min(p[2 * mid - i], ri - i);
        else p[i] = 1;
        while (str[i - p[i]] == str[i + p[i]]) p[i] ++;
        if (ri < i + p[i]) mid = i, ri = i + p[i];
        ans = max(ans, p[i] - 1);
    }
}

3. 时间复杂度的证明

很明显，时间的主要消耗是在 while (str[i - p[i]] == str[i + p[i]]) p[i] ++;。

假设 $p(2\times mid - i) < r - i + 1$，说明我们在匹配 $2 \times mid - i$ 的时候已经发现无法再匹配下去了，而这个无法匹配的字符仍然会被回文到 $i$ 附近，说明匹配 $i$ 的时候，同样会遇到这种情况。那么 while 只会执行一次。

另外的情况，即 $p(2 \times mid - i)\geq r - i + 1$，那么我一直匹配的话，一定会导致 $r$ 跟着增加（因为 $r$ 会被 $i$ 更新）。并且 $r$ 的增加量就是 while 的执行次数。

很明显，$r$ 向右移动的次数不超过 $O(n)$。于是我们证明了 Manacher 就是 $O(n)$。