mydcwfy's Blog

费用流

Posted on
Symbols count in article: 11k Reading time ≈ 24 mins.

比较重要并且难想，需要多加练习。

费用流

1.定义

费用流是指所有最大可行流中，费用最小（最大）值。

前提是最大可行流。

给每条边幅赋一个费用，则总费用为：

如果有最大可行流的话，一定有最小费用最大流。

因为可行流满足两个条件：

  1. 满足容量限制；

  2. 满足容量守恒。

但是有一些最小费用无法求出来。

如图，该费用流无法用后面的方法求出来。

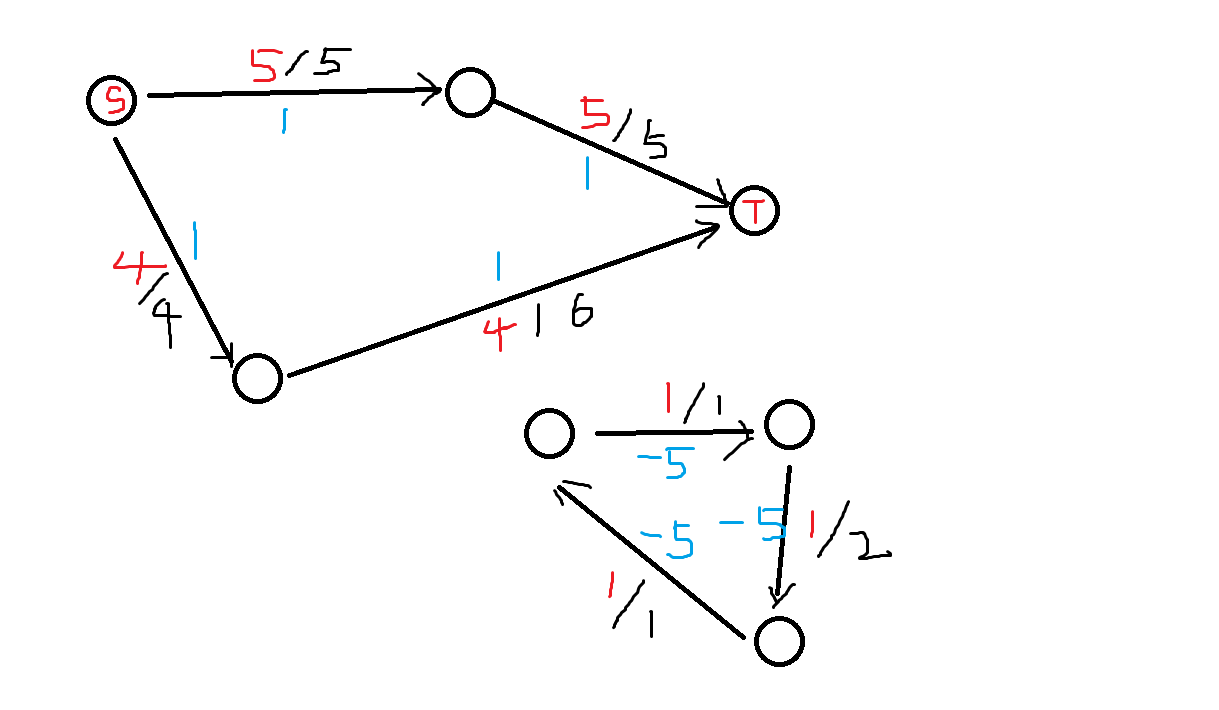
2.求法

Edmonds-Karp 算法为基础。

将 bfs 换为 spfa，这样每一次都是最短路（即最小代价）。

证明：

假设当前的 f1 是最小费用，经过一次 spfa 后，得到 f2，新的为 f

假设 f 不是最小费用，设 f’ 是最小费用，经过 f2‘ 得到。

那么 $|f’|=|f|$。

因为都由 f1 扩展而来，可得 $|f2’|=|f2|$

又$w(f)=|f|*s(f)$，可得 $s(f2’)<s(f2)$，与最短路矛盾。

所以原命题成立。

如果原图有负权回路，那么 spfa 会陷入死循环。

要用到”消圈”的方法，这里不过多赘述。

消圈

建图时，将费用改为$p(u,v)=-p(v,u)$。

一般情况下，只要原图不存在负环，那么残留网络也不会。

（因为流量不会绕圈，所以反向边也不会成环）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void add(int a,int b,ll c,ll d)
{
	e[idx]=b,ne[idx]=h[a],w[idx]=d,f[idx]=c,h[a]=idx++;
	e[idx]=a,ne[idx]=h[b],w[idx]=-d,f[idx]=0,h[b]=idx++;
}

queue <int> q;

bool spfa()
{
	for (int i=0;i<=n;++i) vis[i]=0,d[i]=INF;
	while (!q.empty()) q.pop();
	q.push(S);d[S]=0;flow[S]=INF;
	while (!q.empty())
	{
		int x=q.front();q.pop();
		vis[x]=0;
		for (int i=h[x];~i;i=ne[i])
			if (f[i]&&(d[e[i]]>d[x]+w[i]))
			{
				d[e[i]]=d[x]+w[i];
				pre[e[i]]=i;
				flow[e[i]]=min(flow[x],f[i]);
				if (!vis[e[i]]) q.push(e[i]);
				vis[e[i]]=1;
			}
	}
	return d[T]!=INF;
}

void EK()
{
	while (spfa())
	{
		ll flowd=flow[T];
		maxflow+=flowd;mincost+=flowd*d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			f[pre[i]]-=flowd;
			f[pre[i]^1]+=flowd;
		}
	}
}

3.做题方式

与最大流相似，都是先将原问题转化为一个网络流，然后证明解是一一对应的，最后证明原答案与新图的答案是相关的。

4.例题

T1:

Luogu P4015 运输问题

先建立一个流网络，从源点到仓库建立 $a(i),0$ 的边，从零售店到汇点建立 $b(i),0$ 的边，从仓库到零售店建立 $+\infty,c(i,j)$ 的边。

易得，最大流一定是满流（因为中间都是 $+\infty$）。

证明略，比较容易。

又因为，只有从仓库到零售店的流才会花费，所以最小费用就是原问题的费用。

注意最小最大费用流都要求。

我用传参的方式防止了代码过长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;

const int N=510,M=4e5+10,INF=1e9;
int h[N],e[M],ne[M],w[M],f[M],idx;
int pre[N],d[N],flow[N],c,maxflow;
bool vis[N];
int n,m,S,T;

void add(int a,int b,int c,int d)
{
	e[idx]=b,ne[idx]=h[a],w[idx]=d,f[idx]=c,h[a]=idx++;
	e[idx]=a,ne[idx]=h[b],w[idx]=-d,f[idx]=0,h[b]=idx++;
}

queue <int> q;

bool cmp(int a,int b,int op)
{
	if (op) return a<b;
	return a>b;
}

bool spfa(int op)
{
	for (int i=0;i<=n+m+1;++i) vis[i]=0,d[i]=(op==1?-1:1)*INF;
	while (!q.empty()) q.pop();
	q.push(S);d[S]=0;flow[S]=INF;
	while (!q.empty())
	{
		int x=q.front();q.pop();
		vis[x]=0;//cout<<x<<endl;
		for (int i=h[x];~i;i=ne[i])
			if (f[i]&&cmp(d[e[i]],d[x]+w[i],op))
			{
				d[e[i]]=d[x]+w[i];
				pre[e[i]]=i;
				flow[e[i]]=min(flow[x],f[i]);
				if (!vis[e[i]]) q.push(e[i]);
				vis[e[i]]=1;
			}
	}
	return d[T]!=(op==1?-1:1)*INF;
}

void initing()
{
	for (int i=0;i<idx;i+=2) f[i]+=f[i^1],f[i^1]=0;
}

void EK(int op)
{
	c=maxflow=0;
	initing();
	while (spfa(op))
	{
		int flowd=flow[T];
		maxflow+=flowd;c+=flowd*d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			f[pre[i]]-=flowd;
			f[pre[i]^1]+=flowd;
		}
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n>>m;
	int x;S=0,T=m+n+1;
	for (int i=1;i<=n;++i)
	{
		scanf("%d",&x);
		add(S,i,x,0);
	}
	for (int i=1;i<=m;++i)
	{
		scanf("%d",&x);
		add(i+n,T,x,0);
	}
	for (int i=1;i<=n;++i)
		for (int j=1;j<=m;++j)
		{
			scanf("%d",&x);
			add(i,j+n,INF,x);
		}
	EK(0);cout<<c<<endl;
	EK(1);cout<<c<<endl;
	return 0;
}

T2:

Luogu P4016 负载平衡问题

可以发现，如果一个站比平均值多，他就要输出，否则就要输入。

可以将货物看为流量，将站分为2个部分，但是不是所有边都是连接两部的，也有一部之间的。

最小费用最大流即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;

const int N=105,M=1e4+10,INF=1e9;
int h[N],e[M],ne[M],w[M],f[M],idx;
int pre[N],d[N],flow[N];
int n,S,T,maxflow,mincost,a[N];
bool vis[N];

void add(int a,int b,int c,int d)
{
	e[idx]=b,ne[idx]=h[a],w[idx]=d,f[idx]=c,h[a]=idx++;
	e[idx]=a,ne[idx]=h[b],w[idx]=-d,f[idx]=0,h[b]=idx++;
}

queue <int> q;

bool spfa()
{
	for (int i=0;i<N;++i) vis[i]=0,d[i]=INF;
	while (!q.empty()) q.pop();
	q.push(S);d[S]=0;flow[S]=INF;
	while (!q.empty())
	{
		int x=q.front();q.pop();
		vis[x]=0;
		for (int i=h[x];~i;i=ne[i])
			if (f[i]&&(d[e[i]]>d[x]+w[i]))
			{
				d[e[i]]=d[x]+w[i];
				pre[e[i]]=i;
				flow[e[i]]=min(flow[x],f[i]);
				if (!vis[e[i]]) q.push(e[i]);
				vis[e[i]]=1;
			}
	}
	return d[T]!=INF;
}

void EK()
{
	while (spfa())
	{
		int flowd=flow[T];
		maxflow+=flowd;mincost+=flowd*d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			f[pre[i]]-=flowd;
			f[pre[i]^1]+=flowd;
		}
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n;
	for (int i=1;i<=n;++i) scanf("%d",a+i);
	int sum=0;S=0,T=n+1;
	for (int i=1;i<=n;++i) sum+=a[i];
	sum/=n;
	for (int i=1;i<=n;++i)
		if (sum>a[i]) add(i,T,sum-a[i],0);
		else add(S,i,a[i]-sum,0);
	for (int i=1;i<n;++i)
	{
		add(i,i+1,INF,1);add(i+1,i,INF,1);
	}
	add(1,n,INF,1);add(n,1,INF,1);
	EK();cout<<mincost<<endl;
	return 0;
}

T3:

Luogu P4014 分配问题

和第一题类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;

const int N=105,M=4e5+10,INF=1e9;
int h[N],e[M],ne[M],w[M],f[M],idx;
int pre[N],d[N],flow[N],c,maxflow,S,T;
int n;
bool vis[N];

void add(int a,int b,int c,int d)
{
	e[idx]=b,ne[idx]=h[a],w[idx]=d,f[idx]=c,h[a]=idx++;
	e[idx]=a,ne[idx]=h[b],w[idx]=-d,f[idx]=0,h[b]=idx++;
}

queue <int> q;

bool cmp(int a,int b,int op)
{
	if (op) return a<b;
	return a>b;
}

bool spfa(int op)
{
	for (int i=0;i<=n+n+1;++i) vis[i]=0,d[i]=(op==1?-1:1)*INF;
	while (!q.empty()) q.pop();
	q.push(S);d[S]=0;flow[S]=INF;
	while (!q.empty())
	{
		int x=q.front();q.pop();
		vis[x]=0;//cout<<x<<endl;
		for (int i=h[x];~i;i=ne[i])
			if (f[i]&&cmp(d[e[i]],d[x]+w[i],op))
			{
				d[e[i]]=d[x]+w[i];
				pre[e[i]]=i;
				flow[e[i]]=min(flow[x],f[i]);
				if (!vis[e[i]]) q.push(e[i]);
				vis[e[i]]=1;
			}
	}
	return d[T]!=(op==1?-1:1)*INF;
}

void initing()
{
	for (int i=0;i<idx;i+=2) f[i]+=f[i^1],f[i^1]=0;
}

void EK(int op)
{
	initing();
	c=maxflow=0;
	initing();
	while (spfa(op))
	{
		int flowd=flow[T];
		maxflow+=flowd;c+=flowd*d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			f[pre[i]]-=flowd;
			f[pre[i]^1]+=flowd;
		}
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n;
	int x;S=0,T=2*n+1;
	for (int i=1;i<=n;++i)
		for (int j=1;j<=n;++j)
		{
			scanf("%d",&x);
			add(i,n+j,1,x);
		}
	for (int i=1;i<=n;++i) add(S,i,1,0);
	for (int j=1;j<=n;++j) add(j+n,T,1,0);
	EK(0);cout<<c<<endl;
	EK(1);cout<<c<<endl;
	return 0;
}

T4:

P4013 数字梯形问题

只是要拆点。

同样的建图，只不过这道题比较麻烦，需要处理3个问。

主要讲一下 3 个问题的衔接。

第一个转到第二个时，我们将所有点内的边都设为 $+\infty$

第二个转到第三个时，我们将所有点间的点再都设为 $+\infty$

但是由于每个出发点只能有一次出发，所以不能更新。

看代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define get(i,j) (m+m+i-2)*(i-1)/2+j
using namespace std;

const int N=1e4+10,M=5e5+10,INF=1e9;
int h[N],e[M],ne[M],w[M],f[M],idx;
int pre[N],d[N],flow[N];
int n,m,S,T,maxflow,maxcost,a[N][N];
bool vis[N];

void add(int a,int b,int c,int d)
{
	e[idx]=b,ne[idx]=h[a],w[idx]=d,f[idx]=c,h[a]=idx++;
	e[idx]=a,ne[idx]=h[b],w[idx]=-d,f[idx]=0,h[b]=idx++;
}

queue <int> q;

bool spfa()
{
	for (int i=0;i<N;++i) vis[i]=0,d[i]=-INF;
	while (!q.empty()) q.pop();
	q.push(S);d[S]=0;flow[S]=INF;
	while (!q.empty())
	{
		int x=q.front();q.pop();
		vis[x]=0;
		for (int i=h[x];~i;i=ne[i])
			if (f[i]&&(d[e[i]]<d[x]+w[i]))
			{
				d[e[i]]=d[x]+w[i];
				pre[e[i]]=i;
				flow[e[i]]=min(flow[x],f[i]);
				if (!vis[e[i]]) q.push(e[i]);
				vis[e[i]]=1;
			}
	}
	return d[T]!=-INF;
}

void EK()
{
	maxflow=maxcost=0;
	while (spfa())
	{
		int flowd=flow[T];
		maxflow+=flowd;maxcost+=flowd*d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			f[pre[i]]-=flowd;
			f[pre[i]^1]+=flowd;
		}
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>m>>n;int tot=(m+n-1+m)*n/2,idx1,idx2,idx0;
	S=0,T=2*tot+1;
	for (int j=1;j<=m;++j) add(S,get(1,j),1,0);
	idx0=idx;//开始的边 
	for (int j=1;j<=m+n-1;++j) add(get(n,j)+tot,T,1,0);
	for (int i=1;i<=n;++i)
		for (int j=1;j<m+i;++j) scanf("%d",&a[i][j]);
	for (int i=1;i<=n;++i)
		for (int j=1;j<m+i;++j) add(get(i,j),get(i,j)+tot,1,a[i][j]);
	idx1=idx;
	
	for (int i=1;i<n;++i)
		for (int j=1;j<m+i;++j)
			add(get(i,j)+tot,get(i+1,j),1,0),add(get(i,j)+tot,get(i+1,j+1),1,0);
	idx2=idx;
	
	EK();cout<<maxcost<<endl;
	
	for (int i=0;i<idx;i+=2) f[i]+=f[i^1],f[i^1]=0;//初始化 
	for (int i=idx0;i<idx1;i+=2) f[i]=INF;//点内的边设为INF 
	EK();cout<<maxcost<<endl;
	
	for (int i=0;i<idx;i+=2) f[i]+=f[i^1],f[i^1]=0;
	for (int i=idx1;i<idx2;i+=2) f[i]=INF;//点间的边设为INF 
	EK();cout<<maxcost<<endl;
	
	return 0;
}

T5:餐巾计划问题

题目传送门 Luogu

题目传送门 AcWing

对于每一天，干净毛巾的毛巾只可能来自 3 种情况：

  1. 新买的

  2. 快洗部

  3. 慢洗部

脏的毛巾也只可能来自3种情况：

  1. 留到下一天

  2. 送到慢洗部

  3. 送到快洗部

我们可以将每天用完的旧毛巾看做点，将每天要用的新毛巾看做另外的点

新毛巾就可以从 $s$ 到该点，费用为 $p$

每天都要从该点流 $r(i)$ 到汇点，相当于用了 $r(i)$

快洗与慢洗就相应连到相应相应早上的点。

从 $s$ 到晚上的点流量为 $r(i)$，相当于得到 $r(i)$ 条旧毛巾。

从早上的点到汇点一定是满流，否则就会使货不应求。

但源点开始的点可以不用满流（可以浪费）。

并且，前一天的脏毛巾可以留到下一天。

综上，建图如下（设早上点为$a(i)$，晚上点为 $b(i)$）：

  1. $add(s,b(i),r(i),0)$

  2. $add(a(i),t,r(i),0)$

  3. $add(b(i),b(i+1),+\infty,0)$

  4. $add(s,a(i),+\infty,p)$

  5. $add(b(i),a(i+n),+\infty,s)$

  6. $add(b(i),a(i+m),+\infty,f)$

注意，$s$ 与 $t$ 只是形式上的源汇点，没有什么实际意义，它象征着整个网络流的正常运作，而与本问题无关。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
#define ll long long
using namespace std;

const int N=5e4+10,M=1e6+10,INF=0x7f7f7f7f;
int h[N],e[M],ne[M],f[M],w[M],idx;
int pre[N],n,S,T,flow[N],d[N];
bool vis[N];
ll mincost;

queue <int> q; 

void add(int a,int b,int c,int d)
{
	e[idx]=b,ne[idx]=h[a],f[idx]=c,w[idx]=d,h[a]=idx++;
	e[idx]=a,ne[idx]=h[b],f[idx]=0,w[idx]=-d,h[b]=idx++;
}

bool spfa()
{
	for (int i=0;i<=2*n+1;++i) d[i]=INF,vis[i]=0;
	while (!q.empty()) q.pop();
	q.push(S);d[S]=0;flow[S]=INF;
	while (!q.empty())
	{
		int x=q.front();q.pop();
		vis[x]=0;
		for (int i=h[x];~i;i=ne[i])
			if (f[i]&&d[e[i]]>d[x]+w[i])
			{
				d[e[i]]=d[x]+w[i];
				pre[e[i]]=i;flow[e[i]]=min(flow[x],f[i]);
				if (!vis[e[i]]) q.push(e[i]),vis[e[i]]=1;
			}
	}
	return d[T]!=INF;
}

void EK()
{
	while (spfa())
	{
		int ff=flow[T];
		mincost+=(ll)ff*d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			f[pre[i]]-=ff;
			f[pre[i]^1]+=ff;
		}
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n;
	int a,b,c,d,e;
	S=0,T=2*n+1;
	for (int i=1;i<=n;++i)
	{
		scanf("%d",&a);
		add(i,T,a,0);
		add(S,i+n,a,0);
	}
	cin>>a>>b>>c>>d>>e;
	for (int i=1;i<=n;++i) add(S,i,INF,a);
	for (int i=1;i<=n;++i)
	{
		if (i+1<=n) add(i+n,i+n+1,INF,0);
		if (i+b<=n) add(i+n,i+b,INF,c);
		if (i+d<=n) add(i+n,i+d,INF,e);
	}
	EK();
	cout<<mincost<<endl;
	return 0;
}