CF337C

还是比较好想的，感觉难度应该在黄至绿之间。

话说这道题怎么没人做啊……

如果有没有考虑到的，请轻喷作者 qwq

题意

• 给出 $n$ 道题，答对了 $m$ 道题，按照规则安排 $m$ 道题的顺序，使得分数最小。输出对 $10^9+9$ 取模后的值。
• 从前向后扫描，答对一道分数加 $1$，计数器 $cnt$ 加一，如果 $cnt=k$，那么当前分数翻倍，$cnt$ 清零。如果答错 $cnt$ 清零。
• $2\leq k\leq n\leq10^9,0\leq m\leq n$。

思路

我们首先考虑的肯定是尽量让 $m$ 道题目被翻倍的次数最少。

首先，一种情况是我们间隔开 $m$ 道题，使得每一道题都不会翻倍，那么答案就是 $m$。

具体就是 $k-1$ 道对，$1$ 道错，排列下去最后可以不需要 $1$ 道错误。

判断条件就是 $(n-m+1)\cdot(k-1)\geq m$。

第二种情况就是不得不要翻倍。

考虑第二个样例：

input:
5 4 2
output:
6

我们发现，不论怎么放错误的那个，一定都会有 $2$ 个会相连。（三个相连可以拆分为 $2+1$

那么，让相连的放在哪呢？

如果放在后面的话，一定会使答案变大，所以肯定放在最前面，让翻倍的尽量少。

所以，就可以构造成这样了：

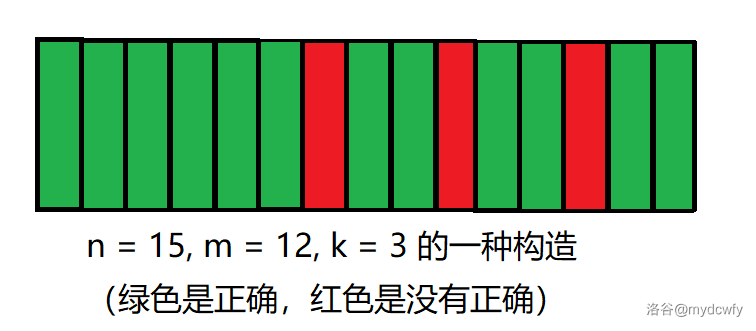
注意到，前面会有 $n-(n-m)\cdot k$ 个连续的绿色。

按照这样计算即可.

假设前面有 $t$ 个连续的 $k$ 个绿色，前面的绿色的贡献就是 $k\cdot2^t+k\cdot2^{t-1}+…+k\cdot2$，注意最后未满 $k$ 个的由于没有特殊贡献，可以放到后面计算，为 $m-t\cdot k$。

前面的式子可以化简为 $k\cdot(2^{t+1}-2)$，快速幂即可。

代码

int main()
{
	cin >> n >> m >> k;
	if ((n - m + 1) * (k - 1) >= m)
	{
		cout << m << endl;
		return 0;
	}
	ll t = (m - (n - m) * (k - 1)) / k;
	printf("%lld\n", (k * (qpow(2, t + 1) - 2 + Mod) % Mod + m - k * t) % Mod);
	return 0;
}