代码简单。
1.定义
即”一笔画“问题,从一个点出发,能不重复地走过所有边,则称该路径为欧拉路径。
如果能走回原点,则该路径为欧拉回路。
注意,点是可以多次经过的,只要不重复走边即可。
2.定理
前提是图连通。
1)无向图
一个图有欧拉回路的充要条件是:该图的每一个点的度数都为偶数。
欧拉路径的充要条件是:除了起始点和终点的度数为奇数,其余都为偶数,或者是欧拉回路。
即:度数为奇数的点只有 0 或 2 个。
必要性易证:如果原命题不成立,每一次经过一个点,需要消耗 2 个度,则有些点度数为奇数的点进来后就没有出去的边了,就没法构成欧拉路径了。
2)有向图
欧拉回路的充要条件是:每一个点的入度和出度都相等。
欧拉路径的充要条件是:要么是欧拉回路,或者除了起点的出度比入度多一,终点的入度比出度多一,其余的点入度和出度相等。
必要性和上面的证明类似。
3.定理充分性的证明
只要对于每个符合条件的图,只要构造出来即可。
通过 dfs 实现。
直接 dfs,但是有一个问题:如果没有找到所有的边怎么办?
首先,可以明确的是,欧拉路径是又若干个环所组成的。
那么,我们怎样将所有的边接为一个大环呢?
我们模拟栈的回溯过程,将第二个环嵌在第一个环中间。
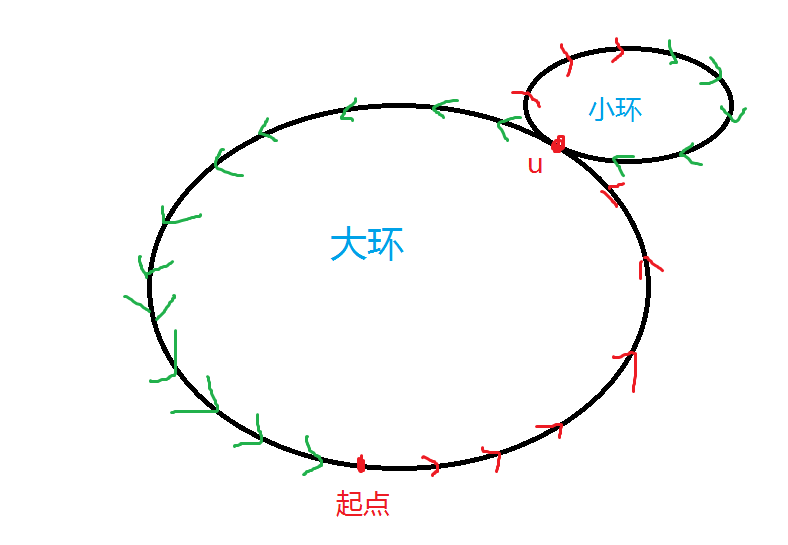
这个会按照 红-绿 的颜色进行递归的,然后按照这个倒序的话,我们就可以找到这个欧拉回路,也就是这个 红-绿 路径。
栈的模拟十分简单,回溯的时候直接将这条边入栈,最后倒序输出就可以了。
但是,这样的时间复杂度是 $O(nm)$(虽然和 spfa 差不多),我们很多时候需要优化,变为严格 $O(n+m)$。
可以发现,每一次前面遍历过的边,都肯定不会再被用到。
直接将 $head[x]$ 设为当前边的下一条 $next[i]$。
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| #include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=4e5+10,M=4e5+10;
int h[N],e[M],ne[M],idx;
int din[N],dout[N],ans[M],cnt;
int n,m,t;
bool vis[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int x)
{
for (int &i=h[x];~i;)
{
if (vis[i])
{
i=ne[i];
continue;
}
vis[i]=1;
if (t==1) vis[i^1]=1;
int now;
if (t==1)
{
now=i/2+1;
if (i&1) now=-now;
}
else now=i+1;
int j=e[i];
i=ne[i];
dfs(j);
ans[++cnt]=now;
}
}
int main()
{
memset(h,-1,sizeof h);
cin>>t>>n>>m;
int a,b;
for (int i=0;i<m;++i)
{
scanf("%d %d",&a,&b);
add(a,b);dout[a]++;din[b]++;
if (t==1) add(b,a);
}
if (t==1)
{
for (int i=1;i<=n;++i)
if (din[i]+dout[i]&1)
{
puts("NO");
return 0;
}
}
else
{
for (int i=1;i<=n;++i)
if (din[i]!=dout[i])
{
puts("NO");
return 0;
}
}
for (int i=1;i<=n;++i)
if (~h[i])
{
dfs(i);break;
}
if (cnt<m)
{
puts("NO");
return 0;
}
puts("YES");
for (int i=cnt;i;i--)
printf("%d ",ans[i]);
return 0;
}
|
