P5088

杂题，没有什么说的。

1. 题意

原题面

抽象一下题意：

求 $k1,k2$，使得：

$$k1\times N:k2\times M=A:B$$

（先使 $\gcd(A,B)=1$

然后，题目要求的就是 $k1+k2-2$ 的最小值。

对应到原题意是什么呢？

我们假设有无穷多个这样的 $N\times M$ 的矩形，然后我们不反射，直接穿过，直到碰到交界的点为止。

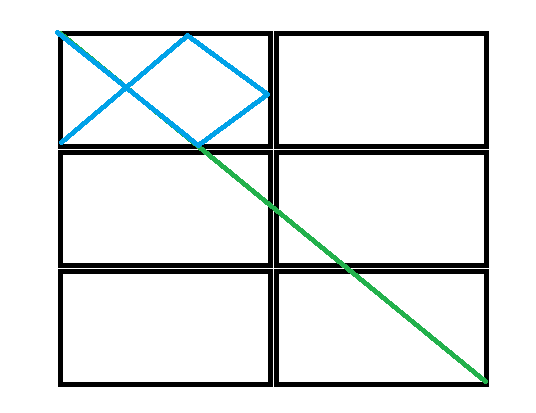
蓝线是原来的反射路径，但是我们可以通过一系列的翻折，使得路径变为绿线。

变为绿线，其实已经简洁了许多。

我们假设横向的有 $k1$ 个 $N$，纵向的有 $k2$ 个 $M$，那么最后 $\zeta$ 的对边是 $k2\times M$，邻边是 $k1\times N$。

于是，我们可以得到：

$$\cot\zeta=\dfrac{k1\times N}{k2\times M}=\dfrac{A}{B}$$

也就是上面的式子了。

至于反射了多少次，其实就是穿过边界了多少次。

大眼观察法易得 $ans=k1+k2-2$。

问题转化为怎样求 $k1,k2$。

首先，可以得到一个解：$k1=A\times M,k2=B\times N$。

然后，我们可以同时除以一个数 $x$。

那么需要满足：$x|A\times M,x|B\times N$。（不然的话，$k1,k2$ 无法整除 $x$，就不是整数了）。

综上，我们其实就可以总结出这道题的答案了：

$$ans=\dfrac{A\times M+B\times N}{\gcd(A\times M,B\times N)}$$

2. 代码

数据水了一点，没有卡掉 long long。

唯一注意的是 $A=0$ 或 $B=0$ 的情况。

int main()
{
	read(n, m, a, b);
	if (a == 0 || b == 0) return puts("0"), 0;
	ll g = Gcd(a, b);
	a /= g, b /= g;
	ll x = Gcd(a * m, b * n);
	write(a * m / x + b * n / x - 2);
	return 0;
}