mydcwfy's Blog

P5192

Posted on
Symbols count in article: 5.4k Reading time ≈ 12 mins.

同步发表于 P5192 题解。

1. 知识储备

网络流 + 最大流。

（如果各位 dalao 已经滚瓜烂熟，请跳过）。

1. 网络流

通俗的讲，网络流就是一个水系，有源点（水库， S ）和汇点（大海， T ），中间有很多节点，中间的节点不储存流，作为一个中转站。

每一条边有一个容量（河道宽度），也有一个流量。显然流量小于等于容量。

如图是一张网络流。

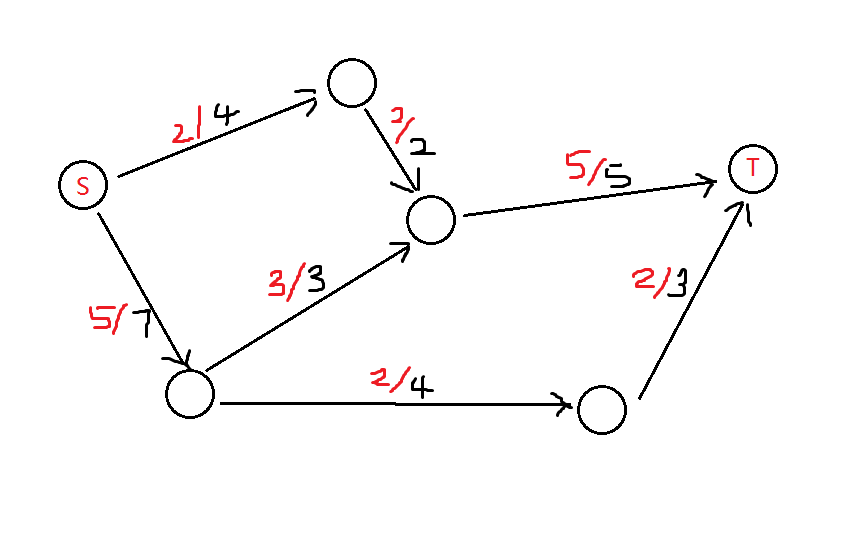
已经有流量的图被称为残留网络。

注意：残留网络中，有反向边，而一般认为原图中没有反向边。
反向边的容量是正向边的流量。

（可以这么认为，反向边是用来退回正向边的流量，而最多就退回原来流过的量）

刚才那张图的残留网络是如下：

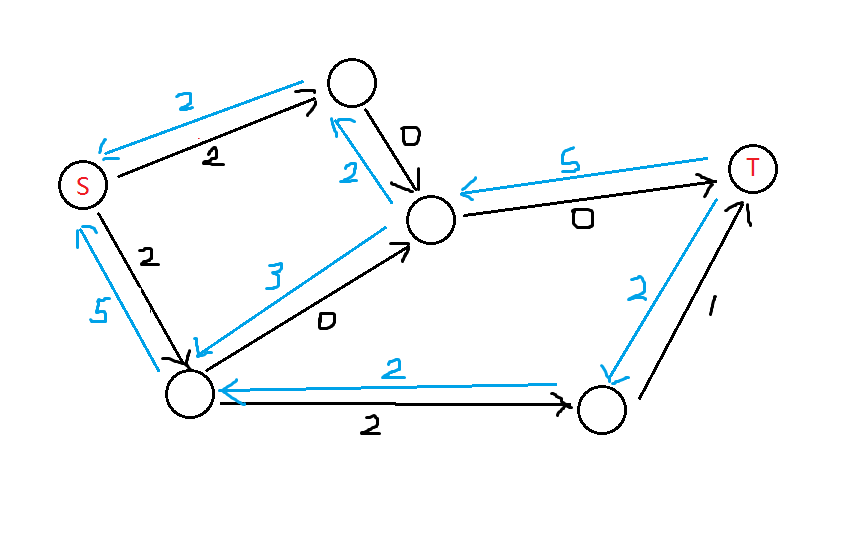
增广路：沿着容量大于0的边，从 S 到达 T 的路径，

（这么多已经足够，详细解释请见百度 逃 ）

2. 最大流

我们现在想要求从源点到汇点能流的最大值。

显然，上面的那张图不是最大流。

最大流应该是这样。

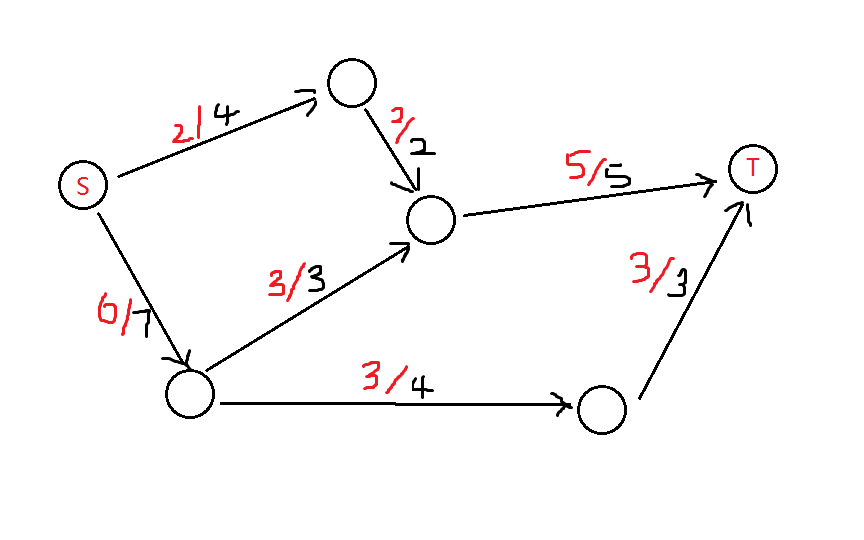
3. Edmonds-Karp 与 Dinic ——求最大流的算法

Edmonds-Karp 的主要思路是每次寻找一条增广路。

原理可以理解为搜索，直到流不过去为止。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

queue<int> q;

bool bfs()// 广搜
{
	for (int i=0;i<N;++i) vis[i]=0;
	d[S]=1e8;
	while (q.size()) q.pop();
	vis[S]=1;
	q.push(S);
	while (q.size())
	{
		int x=q.front();q.pop();
		for (int i=h[x];i!=-1;i=ne[i])
		{
			if (vis[e[i]]) continue;
			if (w[i]!=0)
			{
				vis[e[i]]=1;
				d[e[i]]=min(d[x],w[i]);
				pre[e[i]]=i;//记录前驱
				if (e[i]==T) return true;
				q.push(e[i]);
			}
		}
	}
	return false;
}

int Edmonds_Karp()
{
	int r=0;
	while (bfs())
	{
		int f=d[T];
		for (int i=T;i!=S;i=e[pre[i]^1])
		{
			w[pre[i]]-=f;
			w[pre[i]^1]+=f;//反向边加上对应流量
		}
		r+=f;
	}
	return r;
}

Dinic 是 EK 的优化，主要思想是建立分层图，一次找多个增广路

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
queue <int> q;

bool bfs()
{
    memset(d,-1,sizeof d);
    while (q.size()) q.pop();
    q.push(S);
    d[S]=0;cur[S]=h[S];//cur 是指当前到的出边
    while (q.size())
    {
        int t=q.front();q.pop();
        
        for (int i=h[t];i!=-1;i=ne[i])
        {
			if (d[e[i]]==-1&&w[i])
			{
				d[e[i]]=d[t]+1;
				cur[e[i]]=h[e[i]];
				if (e[i]==T) return true;
				q.push(e[i]);
            }
        }
    }
    return false;
    
}

int find(int u,int lim)
{
    if (u==T) return lim;
    int flow=0;
    for (int i=cur[u];i!=-1&&flow<lim;i=ne[i])
    {
        cur[u]=i;// 当前弧优化，下一次从这一条边出发
        if (d[e[i]]==d[u]+1&&w[i])
        {
            int t=find(e[i],min(w[i],lim-flow));
            if (t!=0) d[e[i]]=-1;
            // 没有路径，就不再访问，赋值为-1
            w[i]-=t,w[i^1]+=t,flow+=t;
        }
    }
    return flow;
}
int dinic()
{
    int r=0,flow=0;
    while (bfs())
        while (flow=find(S,INF)) r+=flow;
    return r;
}

2. 无源汇上下界最大流

我们当然希望他不要有上下界，所以要转化成普通的最大流。

设边 (u,v) 流量为 f(u,v), 那么有

可以得到：

可以发现，我们直接从 u 连一条 cmax(u,v) - cmin(u,v) 为容量的边即可！

真的可以了吗？（雾）

回顾原来的定义，每一个节点都是要不储存流量的，但这样的话，会导致节点 u 存储的一些流量，为

为了弥补这一缺陷，我们不得不建立一个源点和汇点（其他点无法在流入或流出）

如果该项大于 0 ，我们就从源点连一条边到该点，否则就从该点流出到汇点（别无选择）

于是，我们就可以用最大流了。

还有一个问题，假设从源点不能每一条边都是满流？此时，我们可以发现，如果不是满流，每一个点还是要储存流量，就会导致性质无法满足。

最后的最大流，就是从源点出发的流加上每一条边原来没有计算的流量。

（可以先理解，因为每一个流都会从源点流出，不然就会有其他点不流量守恒了）

Code: 略（主要是不想打）

3. 有源汇上下界最大流

有源汇对于无源汇来说，有一点不同：原来的源点（记为 s ）和汇点（记为 t ）也是不流量守恒的。

显而易见的方法是，从 t 到 s 连一条 $+\infty$ 的边。

然后就先从 S 到 T 用 Dinic ，再 s 到 t 用 Dinic 。
两次的流量相加，就可以了。（就可以了）

但真的可以吗？（雾）

是可以的（不要被我问一次就犹豫了）

但是我这里需要严谨证明一下。（看不懂可以略过）

证明

我们需要证明的是原图中从 s 到 t 的可行流与新图第一次 Dinic 后从 s 到 t 的可行流是一 一对应的。

首先，原图的可行流与新图中的满流是一一对应的。

1. 原图至新图

假设新图有一个满流 f(S,T) ，对于任意一个原图的可行流，即一个新图的满流，相减后， S 和 T 相关的边，流量都会变成 0 。

又由于有 c(t,s)=$+\infty$ ，去掉这条边后，就是从 s 到 t 的可行流。

2. 新图至原图

设新图中有一个满流 f(S,T) ，并有任意一个 s 到 t 的可行流 f(s,t).

那么，f(S,T)+f(s,t) 也一定是一个满流，同时由于 f(s,t) 不经过 S 和 T ，每个点也满足流量守恒。

所以对任意一个 f(s,t) ，都有一个满流与之对应，也就是有原图的可行流。

证毕！

4.回归本题

由标题可以看出，本题是一个模板题。

  • 先建立一个源点。
  • 从源点到每个少女，流量为 [gi,$+\infty$)

  • 从每个少女到每一天，流量为 [li,ri]

  • 从每一天到汇点，流量为 [0,di]

记得清零，以及少女的编号问题。

最后，献上代码。其它问题看注释，或者私信。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;

const ll N=5e4+10,M=4e5+10,INF=1e9+7;
ll h[N],e[M],ne[M],w[M],A[N],d[N],cur[N],idx,n,m,S,T,q[N],s,t;

void add(ll a,ll b,ll c)
{
	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
	e[idx]=a,w[idx]=0,ne[idx]=h[b],h[b]=idx++;
}
//加每一个有上下界的边
void addedge(ll from,ll to,ll least,ll most)
{
	add(from,to,most-least);
	A[from]-=least,A[to]+=least;
}

bool bfs()
{
	memset(d,0,sizeof d);
	ll hh=1,tt=1;
	q[tt]=S;d[S]=1;cur[S]=h[S];
	while (hh<=tt)
	{
		ll x=q[hh++];
		for (ll i=h[x];i!=-1;i=ne[i])
			if (!d[e[i]]&&w[i])
			{
				d[e[i]]=d[x]+1;
				cur[e[i]]=h[e[i]];
				if (e[i]==T) return true;
				q[++tt]=e[i];
			}
	}
	return false;
}

inline ll read()
{
	char c;
	ll res=0,f=1;
	while ((c=getchar())<'0'||c>'9')
		if (c=='-') f=-1;
	res=c-'0';
	while ((c=getchar())<='9'&&c>='0') res=(res<<3)+(res<<1)+c-'0';
	return res*f;
}

ll findflow(ll x,ll limit)
{
	
	ll flow=0;
	if (x==T) return limit;
	for (ll i=cur[x];i!=-1&&flow<limit;i=ne[i])
	{
		cur[x]=i;//当前弧优化
		if ((d[e[i]]==d[x]+1)&&w[i])
		{
			ll t=findflow(e[i],min(limit-flow,w[i]));
			if (!t) d[e[i]]=-1000;
			w[i]-=t,w[i^1]+=t,flow+=t;
		}
	}
	return flow;
}
//dinic 模板
ll dinic()
{
	ll r=0,flow;
	while (bfs())
		while (flow=findflow(S,INF)) r+=flow;
	return r;
}

int main()
{
	while (~scanf("%d%d",&n,&m))//敲黑板
	{
		memset(h,-1,sizeof h);
		memset(A,0,sizeof A);//A 是指多出来的流量
		s=0,t=m+n+1;ll tot=0;idx=0;//原图的源汇点
		for (ll i=1,x;i<=m;++i)
		{
			x=read();
			addedge(s,i,x,INF);
		}
		for (ll i=1,C,D;i<=n;++i)
		{
			C=read();D=read();
			addedge(m+i,t,0,D);
			for (ll j=1,x,L,R;j<=C;++j)
			{
				x=read(),L=read(),R=read();
				addedge(x+1,m+i,L,R);
			}
		}
		S=m+n+2;T=m+n+3;//新图的源汇点
		for (ll i=0;i<=m+n+1;++i)
		{
			if (A[i]>0) add(S,i,A[i]),tot+=A[i];
			else if (A[i]<0) add(i,T,-A[i]);
		}
		add(t,s,INF);
		if (dinic()<tot)//判断是否为满流
		{
			puts("-1\n");
			continue;
		}
		ll res=w[idx-1];
		w[idx-1]=w[idx-2]=0;
		S=s,T=t;
		printf("%d\n\n",res+dinic());
	}
	return 0;
}