Tarjan 算法

比较重要的图论，tg 中考得比较多。

1. 定义

连通分量：可以互相到达的点集
强连通分量：极大的连通分量（即不可扩展的）
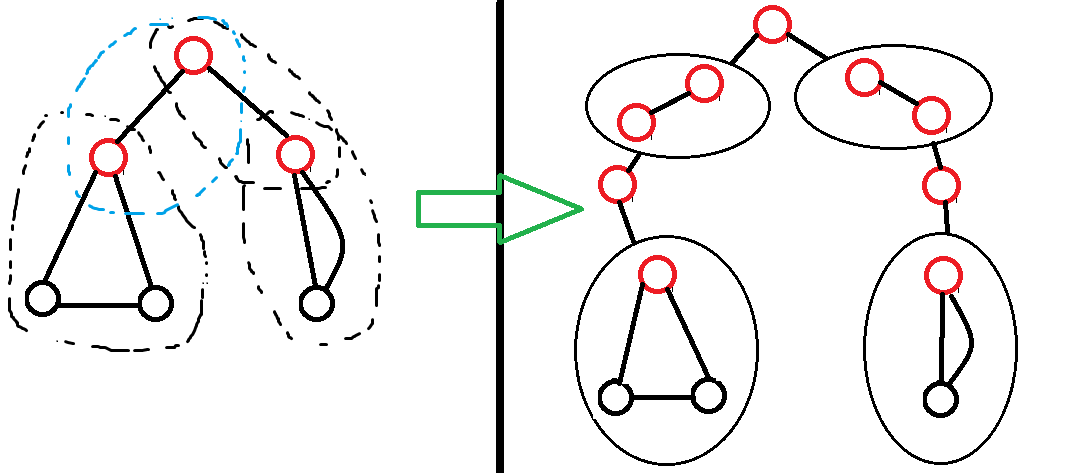
常见应用：缩点，可将有向图变为有向无环图（ DAG ），无向图变为树 / 森林。

2. 求强连通分量（ SCC ）： DFS+Tarjan

注意，下面的定义是属于有向图的，无向图等一下再讨论！

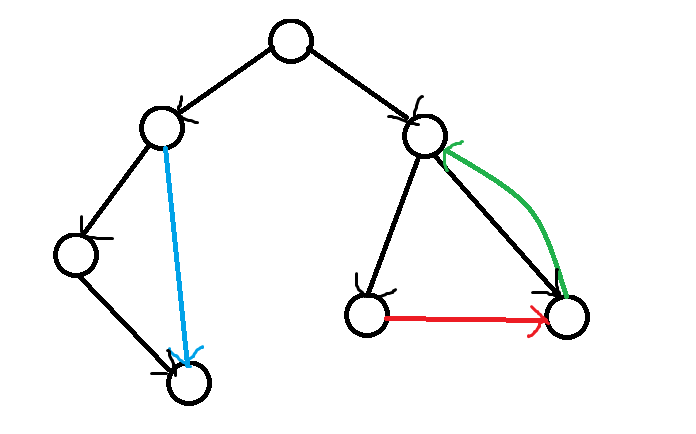
1) DFS 的特殊定义

边可分为4类：

树枝边：搜索时所经历的边（树枝边构成树）
前向边：祖先指向儿子
后向边：儿子指向祖先
横叉边：不属于上面3种的边（大雾）

（黑色为树边，蓝色为前向边，红色为橫叉边，绿色为后向边）

2) 哪些边有用？

后向边：祖先先到儿子，儿子回到了祖先（一定是）
横叉边：点先到另外点，在有横叉边的话可能回到了祖先

3) Tarjan 算法

a. 又是定义（雾）

时间戳（ dfn ）：遍历到 u 的时间点
low ：以 u 为根的子树，只走一条边能到达的 dfn 的最小值
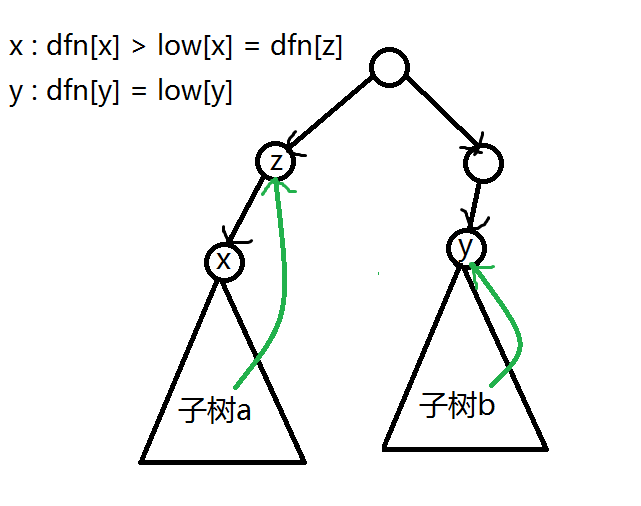
u 是一个强连通分量 dfn 的最小值，等价于 $dfn(u) = low(u)$

b. 算法流程

保存一个栈，是搜到的点
搜索所有相邻的点，如果未搜过，就递归搜索，如果搜过（即不是树枝边），就有 $low(u)=\min (dfn(v),low(u))$
如果 $dfn(u) = low(u)$，将栈里的点一一取出，合并为一个 SCC，直到取出自己
复杂度 $O(m+n)$

c.证明：略（过于复杂）

3. 后续事务

1) 缩点

遍历每一条原图中的边，如果端点不在同一分量中，就将该两个 SCC 连起来

2）在 DAG 上拓扑排序

其实可以不用，因为 SCC 的顺序就是拓扑序的倒序

证明：

拓扑序的第一个，一定会在搜的时候搜到其他的强连通分量，并在该 SCC 前就已经结束，第一个一定是最后搜到的 SCC

4. Code

void Tarjan(int x)
{
	dfn[x]=low[x]=++tot;
	st[++top]=x, ins[x]=true;
	for (int i=h[x];~i;i=ne[i])
    	if (!dfn[e[i]])
    	{
    		Tarjan(e[i]);
			low[x]=min(low[x],low[e[i]]);
    	}
		else if (ins[e[i]]) low[x] = min(low[x], dfn[e[i]]);
	if (low[x]!=dfn[x]) return;
	cnt++;int now;
	do{
		now=st[top--];
		ins[now]=false;// 出栈 
		bel[now]=cnt;
	}while (now!=x);
	return ;
}

void suodian()
{
	for (int x=1;x<=n;++x)
		for (int i=h[x];~i;i=ne[i])
			if (bel[x]!=bel[e[i]]) add(h2, bel[x], bel[e[i]]);
	n=cnt;
}

5. 无向图

既和有向图类似，有和有向图有区别。

首先，边的分类只有 3 种：树边，前向边，后向边。

为什么没有横叉边呢？其实原因很简单，首先，横叉边是指不同子树之间的边。试想，如果有横叉边的话，当我们走到先遍历的点 $u$ 时，另一个子树还没有遍历，那 $u$ 一定会走到 $v$，让横叉边变为了树边了。

注意，这个代码还应该传一个 $fa$,，防止又走回 $fa$ 而导致死循环了。

代码（找不到了……

6. 点双联通分量与边双连通分量

这两个有区别，一般用于无向图。

1）定义

点双连通分量：不存在割点，也就是任意去掉一个点，原图仍然联通。
边双连通分量：不存在桥，也就是任意去掉一条边，原图仍然联通。

还要区分的是，点双连通分量与边双连通分量是互不包含的，这个有些书上可能是讲错了。

2）判定

割点：存在一个点 $v$，使得 $dfn(u)\leq low(v)$（dfs 树的根节点需要两个 $v$），那么 $u$ 是割点。
桥：存在一条边 $e(u,v)$，使得 $dfn(u)<low(v)$，那么 $e(u,v)$ 是桥。

注意两个的判定区别。

3）简要证明

割点：因为 $v$ 所在的子树不可能到达 $u$ 以上的节点了，所以每一个节点向上遍历的话都要经过 $u$，所以 $u$ 删去后会使原图不联通。但如果是根节点的话，没有向上的点了，所以需要多一个 $v$，那么删去根节点后就不联通了。
桥：$v$ 所在的子树不可能到达 $u$ 及以上的节点了，所以删去 $e(u,v)$ 会使 $v$ 的子树与其他不联通， $e(u,v)$ 就是桥了。

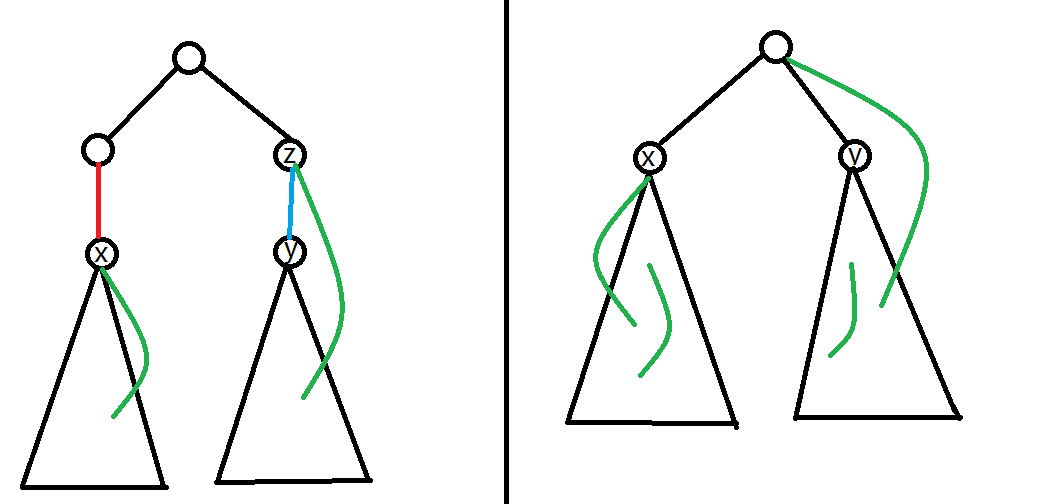
左边的图中，红色的边下面的点 $low(x)=dfn(x)$，$low(x)<dfn(x.fa)$，那么红边就是桥，但 $low(y)=dfn(z)\not<dfn(z)$，所以蓝边 $e(y,z)$ 不是桥。在右边的图中，$x$ 下面的点 $v$ 一定满足 $low(v)\geq dfn(x)$，所以 $x$ 就是割点。而 $y$ 下面的点会有 $low(x)=dfn(root)<dfn(y)$，所以 $y$ 就不是割点。

4）缩点

a. 边双连通分量

这个要简单一些，所以先讲（？

根据定义，不存在桥的子图就是边联通图，而极大的边联通图就是边双连通分量。

（其实和前面的 Tarjan 差不多）~~（废话，前面的无向图 Tarjan 就是边双连通分量）~~

b. 点双连通分量

这个其实要难一些很多

首先，我们将所有的割点处理出来。

如果我们得到 $dfn(u)\leq low(v)$，我们就将当前栈内的所有点一直弹出，直到弹出的点为 $u$，将所有弹出的点都加入一个新的点双连通分量，然后还要将 $u$ 入栈。

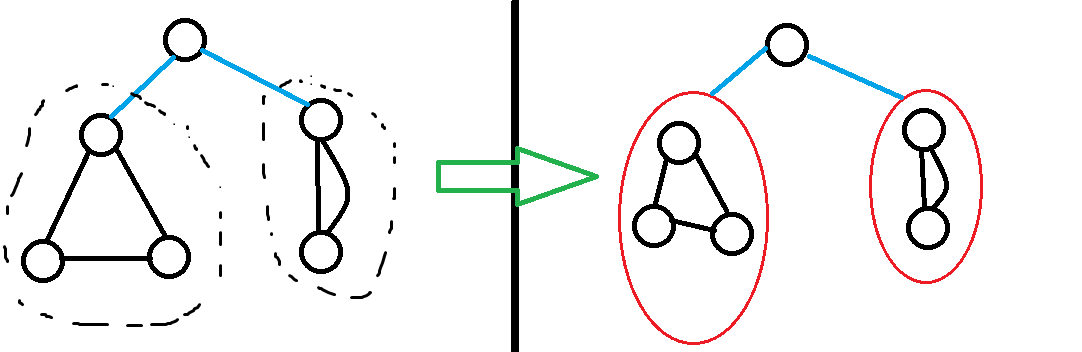
如果要缩为一个新图的话，我们还要注意：每一个割点都是一个新图中的点，然后每一个点双连通分量也是新图中的一个点，连接就是割点向有它的点双连通分量连边。原图最后变为了一棵树（森林）。

缩完点后，就可以树形 DP 了。

int h1[N], h2[N], e[M], ne[M], w[M], idx;//h1 是原图，h2 是新图
int low[N], dfn[N], tot, stk[N], top, cnt;
vector <int> dcc[N];//存每一个点双连通分量的原图编号

void add(int *h, int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void tarjan(int x, int from)
{
	low[x] = dfn[x] = ++ tot, stk[++ top] = x;
	for (int i = h[x]; ~i; i = ne[i])
	{
		if (i == (from ^ 1)) continue;
		if (!dfn[e[i]])
		{
			tarjan(e[i], i);
			if (low[e[i]] <= dfn[x])
			{
				int now;cnt ++;
				while (stk[top] != x)
				{
					now = stk[top --];
					dcc[cnt].push_back(now);
				}
				dcc[cnt].push_back(x);
				add(h2, x, cnt + n);
			}
			low[x] = min(low[x], low[e[i]]);
		}
		else low[x] = min(low[x], dfn[e[i]]);
	}
}

7. 例题

T1： Luogu P2341 受欢迎的牛

题目传送门

如果是一个 DAG 的话，直接是出度为 0 的点就是答案

但是，如果有多个点的话，那么哪个点都不是。

考虑 Tarjan，缩点后出度为 0 的点的大小就是了。

Code:

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;

const int N=1e4+10,M=5e4+10;

int h[N],e[M],ne[M],idx;
int st[N],top,dfn[N],low[N],bel[N],cnt,tot,dout[N],din[N],n,m,s[N];
bool ins[N];

void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void Tarjan(int x)
{
	dfn[x]=low[x]=++tot;
	st[++top]=x, ins[x]=true;
	for (int i=h[x];~i;i=ne[i])
    	if (!dfn[e[i]])
    	{
    		Tarjan(e[i]);
			low[x]=min(low[x],low[e[i]]);
    	}
		else if (ins[e[i]]) low[x] = min(low[x], dfn[e[i]]);
	if (low[x]!=dfn[x]) return;
	cnt++;int now;
	do{
		now=st[top--];
		ins[now]=0; 
		bel[now]=cnt;
		s[cnt]++;
	}while (now!=x);
	return ;
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n>>m;
	int x,y;
	while (m--)
	{
		scanf("%d %d",&x,&y);
		add(x,y);
	}
	for (int i=1;i<=n;++i)
		if (!dfn[i]) Tarjan(i);
	for (int x=1;x<=n;++x)
	{
		for (int i=h[x];~i;i=ne[i])
			if (bel[x]!=bel[e[i]])
			{
				dout[bel[x]]++;
				din[bel[e[i]]]++;
			}
	}
	int b=0;
	for (int i=1;i<=cnt;++i)
	{
		if (!dout[i])
		{
			if (b)
			{
				puts("0");
				return 0;
			}
			b=s[i];
		}
	}
	cout<<b<<endl;
	return 0;
}

T2： AcWing 367 学校网络 / Luogu P2812 校园网络（加强版）

题目传送门_AcWing

题目传送门_Luogu

对于第一问，缩点后，入度点的个数即为答案（这些点必须得到，得到后，所有也都会得到）

对于第二问，设入度为0的点有 $P$ 个，出度为0的点有 $Q$ 个，则答案为

$ans=\max (P,Q)$

证明有很多有些问题，这篇博客证明了（我也不知道有没有问题雾）

证明