需要的初高中几何知识是比较多的。
1. 数学基础
第一个的原理来自于:$\cos \pi = -1$。
第二个是一个余弦定理。
2. 关于浮点数
比如我们比较两个数的时候,他们可能因为计算的误差而不同。所以我们必须定义一个 $\epsilon$,表示两个的差别,如果在 $\epsilon$ 中的话,我们就认为这两个数相等。$\epsilon$ 可以定义为 $10^{-8}, 10^{-9}$ 等等。
1
2
3
4
5
6
| const double eps = 1e-9;
bool is_equal(double x, double y)
{
return fabs(x - y) < eps;
}
|
同样,如果比较两个数的大小,我们同样也要使用 $\epsilon$:
1
2
3
4
5
| int cmp(double x, double y)
{
if (fabs(x - y) < eps) return 0;
return x > y ? 1 : -1;
}
|
3. 向量
首先,简单的向量加减不再展开。
我们先介绍点乘:$a \cdot b = |a||b|\cos$。
如果在二维点坐标下计算,就是 $(a, b) \cdot (c, d) = ac + bd$。
1
2
3
4
| double dot(Point a, Point b)
{
return a.x * b.x + a.y * b.y;
}
|
我们计算一个向量的模的时候,可以直接计算就是了,也可以 $|a| = \sqrt{a \cdot a}$。
1
| double length(Point a){return sqrt(dot(a, a));}
|
我们可以使用点乘来计算两个之间的夹角。
$\cos = \dfrac{a\cdot b}{|a||b|}$。
1
| double get_angle(Point a, Point b){return acos(dot(a) / length(a) / length(b));}
|
还有一种乘法,是叉乘:$a\times b = |a||b|\sin$。
如果是二维点坐标,就是 $(a, b)\times (c, d) = ad - bc$。
如果叉乘大于 0 的话,那么 $a$ 向量在 $b$ 向量的顺时针的方向。注意叉乘没有交换性。一般将叉乘重载为乘法。
1
2
3
4
| double cross(Point a, Point b)
{
return a.x * b.y - a.y * b.x;
}
|
还有一个,我们转一个角。
直接写出公式,证明可以使用和差角公式:
1
2
3
4
| Point rotate(Point a, double c)
{
return {a.x * cos(c) - a.y * sin(c), a.x * sin(c) + a.y * cos(c)};
}
|
4. 计算几何
似乎能写的似乎不多……
我们简单的看几个比较常用的。
1)直线相交
首先,判断两个直线是否相交:$a\times b \not= 0$。
1
| bool is_cross(Point a, Point b){return cross(a, b) != 0;}
|
2)线段相交
分为两步:快速排斥实验和跨立实验。
快速排斥实验是指如果两个线段所在的矩形如果不相交,那么两条线段一定不相交。
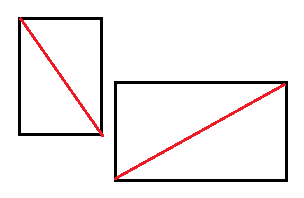
如果两个线段所在的矩形是相交的,也不说明两条线段是相交的。
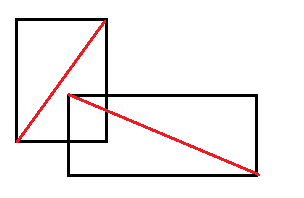
我们需要判断两个线段相交的话,需要判断一个线段的两个点是否在另外一个线段所在直线的两侧。
具体来说,就是判断 $(p3 - p1) \times (p2 - p1)$ 与 $(p4 - p1) \times (p2 - p1)$ 是否异号。
另外,我们可以直接对这两条线段都这么计算,可以省去第一步。
1
2
3
4
5
6
| bool cross_seg(Point p1, Point p2, Point p3, Point p4)
{
if (((p1 - p3) * (p4 - p3)) * ((p2 - p3) * (p4 - p3)) > eps) return 0;
if (((p3 - p1) * (p2 - p1)) * ((p4 - p1) * (p2 - p1)) > eps) return 0;
return 1;
}
|
3)判断一个点是否在多边形内
注意不一定是凸多边形。
有一个结论:经过凸多边形的边奇数次,就在凸多边形内。
很明显,没经过一次边,就会导致从外到内,或者从内到外。最后一定是在外部,所以奇数次的话该点就在里面。
注意这个结论在经过某一个顶点或者射线与边重合时并不适用,所以我们随机一个在凸多边形外部的点判断就可以了。
(不保证代码正确
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| bool in_polygon(Point *p, Point a, int n)
{
p[n + 1] = p[1];
for (int i = 1; i <= n; ++ i)
if (fabs((p[1] - p[i]) * (p[i + 1] - p[i])) < eps &&
dot(p[1] - p[i], p[i + 1] - p[i]) > eps && dot(p[i + 1] - p[1], p[i + 1] - p[i]) > eps)
return 0;
while (1)
{
Point c = {(double)rand(), (double)rand()};
bool flag = 0;
for (int i = 1; i <= n && !flag; ++ i)
if (fabs((c - a) * (p[i] - a)) < eps && fabs((c - a) * (p[i + 1] - a)) < eps)
{
flag = 1;
break;
}
if (flag) continue;
flag = 0;
for (int i = 1; i <= n; ++ i)
flag ^= cross_seg(a, c, p[i], p[i + 1]);
return flag;
}
}
|
4)多边形面积
这是一个结论,我们就不证明了。
1
2
3
4
5
6
7
| bool sum_area(Point *p, int n)
{
double res = 0;
for (int i = 2; i < n; ++ i)
res += (p[i + 1] - p[1]) * (p[i] - p[1]);
return res;
}
|
5. 例题
T1:玩具
题目传送门 POJ
我们二分,找到第一个在该点左边的隔板。判断这个点是否在线段的右边(这里是顺时针方向),直接用叉乘即可。
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
struct Point{
LL x, y;
Point operator +(Point t)const{
return {x + t.x, y + t.y};
}
Point operator -(Point t)const{
return {x - t.x, y - t.y};
}
LL operator *(Point t)const{
return x * t.y - y * t.x;
}
}L, R, now, up[N], dn[N];
int n, m, cnt[N];
int main()
{
bool is_fir = 1;
while (scanf("%d", &n) && n)
{
scanf("%d %lld %lld %lld %lld", &m, &L.x, &R.y, &R.x, &L.y);
up[0] = {L.x, L.y}, dn[0] = {L.x, R.y};
for (int i = 1; i <= n; ++ i)
scanf("%lld %lld", &dn[i].x, &up[i].x);
for (int i = 1; i <= n; ++ i) up[i].y = L.y, dn[i].y = R.y;
for (int i = 0; i <= n; ++ i) cnt[i] = 0;
if (!is_fir) puts("");
for (int cse = 1; cse <= m; ++ cse)
{
scanf("%lld %lld", &now.x, &now.y);
int l = 0, r = n;
while (l < r)
{
int mid = (l + r + 1) >> 1;
if ((now - up[mid]) * (dn[mid] - up[mid]) > 0) l = mid;
else r = mid - 1;
}
cnt[l] ++;
}
for (int i = 0; i <= n; ++ i) printf("%d: %d\n", i, cnt[i]);
is_fir = 0;
}
return 0;
}
|

