Div 2 当场降智,直接变成了 SpeedForces 了。
比赛记录:ABC Accepted,Scores:2247,Rank:872。
改题进度:ABCEF Accepted。
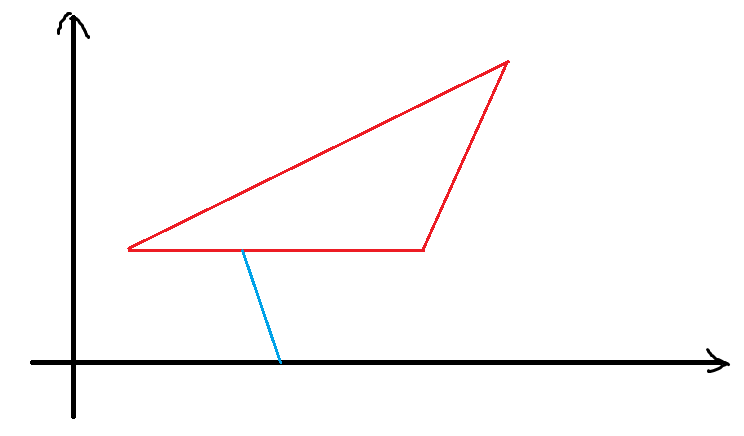
A 题意:给一个三角形,求不能通过不穿过三角形的直线到达 y 轴的线段长度。
显然如果想要不能到达 y 轴,一定是平行于 y 轴的线才有可能。
如果第三个点在这两个点的上方,答案也显然是 0:
按 y 坐标排序即可。
1 2 3 4 5 6 7 8 9 void solve () PDD p[3 ]; for (int i = 0 ; i < 3 ; ++ i) std::cin >> p[i].first >> p[i].second; std::sort (p, p + 3 , [](PDD a, PDD b) { return a.second < b.second ;}); if (p[1 ].second != p[2 ].second) puts ("0" ); else printf ("%.10lf\n" , std::abs (p[1 ].first - p[2 ].first)); }
B 题意:给一个长度为 $n$ 的数组,对于每一个 $k\in[1, n]$,求出划分为 $k$ 个集合后,求每一个集合的不同元素的个数总和的最小值。
显然我们将相同的元素放在一起,答案也至少是这个数组中数的不同的个数 $j$。
显然答案 $\geq k$。尝试证明答案 $ans_k = \max(k, j)$。
当 $k < j$ 的时候,我们将相同的放在一起,会出现 $j$ 个集合,然后任意合并一些,答案不变,所以 $ans_k = j$。
当 $k \geq j$ 的时候,我们仍然将相同的放在一起,然后操作 $k - j$ 次,每一次分裂一个集合。显然答案每次加 1,总答案为 $j + (k - j) = k$。
1 2 3 4 5 6 std::sort (a + 1 , a + n + 1 ); int cnt = 0 ;for (int i = 1 ; i <= n; ++ i) if (a[i] != a[i - 1 ]) cnt ++; for (int i = 1 ; i <= cnt; ++ i) printf ("%d " , cnt);for (int i = cnt + 1 ; i <= n; ++ i) printf ("%d " , i);
C 题意:定义一个数列是好的,为可以划分为 $\dfrac n2$ 对(显然 $n$ 为偶数),每一对中两数之商为 $x$。给一个序列,添加最少的数使得序列是好的。$n\leq 2\cdot 10^5,2\leq x \leq10^6$。
我们直接找到可以匹配的最大对数,让剩下的每一个都加一个数与之匹配即可。问题转化为求最大匹配数。
直接将所有数扔入一个 multiset,然后从小向大枚举。如果还没有匹配的话,说明不能和小的匹配,直接找一个 $a_i \cdot x$,看一下有没有,有就删一个。
最后直接输出 multiset 的 size() 即可。
注意如果只删一个数,应该写为 erase(find(x)) 而不是 erase(x),那样会删掉所有的相同元素。
1 2 3 4 5 6 7 8 std::multiset<int > a; for (auto iter = a.begin (); iter != a.end (); iter ++){ LL now = *iter; auto t = a.find (now * x); if (t != a.end ()) a.erase (t); } printf ("%d\n" , int (a.size ()));
E 题意:你需要猜长度为 $n$ 的 01 序列,每次给定区间的或,或者查询单点是否能确定为 0 还是 1,如果能确定输出结果。$n, q\leq 2\times 10 ^ 5$。
挺有意思的,不过不是很难。
用一个 std::set 维护所有可能为 1 的位置,或和为 0 很好处理,直接将 std::set 中所有 $\in [l, r]$ 的数删去即可。
考虑查询,如果我们这个数没有出现在 std::set 当中,则显然为 0。接下来我们考虑能不能确定为 1。
如果这一个确定为 1 的话,一定满足一个区间或为 1,且在这个区间中有且只有这一个位置可能为 1。那么相当于满足 $l\in [pre + 1, pos]$,$r\in[pos, nxt - 1]$ 是否存在一个区间或为 1。看似动态二维数点,但是其实只需要维护有没有,我们只需要知道 $l\in [pre + 1, pos]$ 中 $r$ 的最小值即可,看他是否 $< nxt$。用一个线段树即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 int main () std::cin >> n >> Q, seg.build (1 , 1 , n); for (int i = 0 ; i <= n + 1 ; ++ i) ms.insert (i); int op, l, r, x; while (Q --) { scanf ("%d %d" , &op, &l); if (op == 0 ) { scanf ("%d %d" , &r, &x); if (!x) { auto iter = ms.lower_bound (l); while (*iter <= r) ms.erase (std::prev (++ iter)); } else seg.modify (1 , l, r); } else { if (!ms.count (l)) { puts ("NO" ); continue ; } else { int t; auto iter = ms.find (l); t = seg.query (1 , *std::prev (iter) + 1 , l); puts (t < *std::next (iter) ? "YES" : "N/A" ); } } } return 0 ; }
F 给定 $n$ 个长度为 $m$ 的数组,每个数组有一个权值 $w$,找到两个数组使得数字没有重复,求这两个数组权值和的最小值。$n \leq 10^5, m\leq 5$,保证一个数组内数字没有重复。
比赛直接降智,胡了个错误的 Tarjan,没想到暴力就过去了……
笔者也不会题解主要介绍的方法 $O(n2^m)$,但是 $O(\dfrac{n^2m}\omega)$ 的算法就是香啊!
我们直接考虑暴力怎么做:直接枚举每一个数,将包含这个数的所有数组互相都设为不可用。即开一个二维 boolean 数组,$a[i][j]$ 表示 $i, j$ 数组能不能选在一起。枚举每一个数时,设包含这个数的数组集合为 $S$,则 $[i \in S][j \in S] a[i][j] \leftarrow 0$。
看到我们只用枚举每个数,我们可以先存下来每一个数对应的 $S$(?,然后枚举到一个数组的时候,直接 &$S$ 即可。时空复杂度均为 $O(\dfrac{n^2m}\omega)$,然后就成功 MLE(还不是最惨的,我加了些优化,变为了 $O(\dfrac {n^2}\omega)$):
怎么办呢?
我们发现,有很多 $S$ 只有一两个位置有 $1$,但是我们却存了不知多少个 0。我们直接考虑设定阈值 $T$,当 $\mid S \mid \leq T$ 时我们直接让 $S$ 暴力更新即可。可以发现,最多有 $\dfrac {nm}T$ 个数我们要开 $\text{bitset}$,所以空间复杂度为 $O(nm + \dfrac{n^2m}{T\omega})$,时间复杂度为 $O(nmT + \dfrac{n^2m}{w})$,取 $T = 500\sim 1000$ 比较合适的样子。(但是我开的 50 也过了
注意指针等的使用,可能有些难写,给出整个代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 const int N = 1e5 + 10 , Block = 1000 ;int n, m;struct Arr { int a[6 ], w; } c[N]; std::bitset<N> bt[505 ], tmp, *bk[N << 3 ], *it = bt; std::vector<int > al, ha[N << 3 ]; int main () std::cin >> n >> m; al.reserve (n * m); for (int i = 1 ; i <= n; ++ i) { for (int j = 1 ; j <= m; ++ j) scanf ("%d" , &c[i].a[j]); scanf ("%d" , &c[i].w); } std::sort (c + 1 , c + n + 1 , [&](const Arr &c1, const Arr &c2) { return c1.w < c2.w; }); for (int i = 1 ; i <= n; ++ i) for (int j = 1 ; j <= m; ++ j) al.push_back (c[i].a[j]); std::sort (al.begin (), al.end ()); al.erase (std::unique (al.begin (), al.end ()), al.end ()); int sz = al.size (); for (int i = 1 ; i <= n; ++ i) for (int j = 1 ; j <= m; ++ j) c[i].a[j] = std::lower_bound (al.begin (), al.end (), c[i].a[j]) - al.begin () + 1 ; for (int i = 1 ; i <= n; ++ i) for (int j = 1 ; j <= m; ++ j) ha[c[i].a[j]].push_back (i); for (int i = 1 ; i <= sz; ++ i) { if (ha[i].size () <= Block) continue ; bk[i] = it ++, bk[i]->set (); for (int pos : ha[i]) bk[i]->reset (pos); } int ans = 2e9 + 7 , t; for (int i = 1 ; i <= n; ++ i) { std::bitset<N> now; now.set (); for (int j = 1 ; j <= m; ++ j) if (ha[c[i].a[j]].size () <= Block) for (int pos : ha[c[i].a[j]]) now[pos] = 0 ; else now &= *bk[c[i].a[j]]; if ((t = now._Find_next(0 )) <= n) ans = std::min (ans, c[i].w + c[t].w); } puts ("-1" ); return 0 ; }