贪心做多了,E 题 DP 也认为是贪心(自然挂了却死活找不出错
个人感觉 D 比 E 简单,怎么 D 比 E 少那么多人?
赛时进度:ABCDE Accepted,Penalty:214,Rank:86。
改题进度:All Accepted。
A
题意:求一个数组长度最小,且满足有 $[l_1, r_1]$ 个最小值,$[l_2, r_2]$ 个最大值。
判一下区间有没有交即可。否则就是 $l_1 + l_2$。
B
题意:给定 $n\times m$ 的网格,有些格子有机器人,每次操作会让所有机器人移动同样的方向,问能否在所有机器人都不出格子的情况下有一个机器人走到最左上 $(1, 1)$。
容易发现下图情况一定不行:
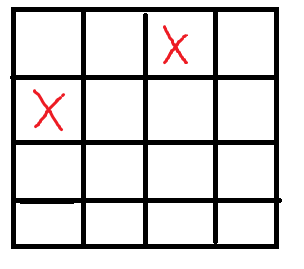
你无法将其中的任意一个移到左上方。
所以这样你只需要找到最靠左上的,判一下剩下的点是否在他的右下方,这样就可以看出是否合法了。
C
题意:给定一个 01 字符串,可以从前后删除一些数,使得剩下的 0 的个数和删除 1 的个数最大值最小。$n\leq 10 ^ 5$。
容易发现最大值最小,果断二分。
然后首先 0 的个数满足条件需要我们双指针到最远的位置,在判是否删除 1 的个数大于限制。时间复杂度 $O(n\log n)$。
D
题意:给定一个序列,为 0 表示不知道,你需要将每一个 0 替换为 $[-k, k]$ 的一个数,使得和为 0,且前缀最大值 - 前缀最小值最大。输出前缀最大值 - 前缀最小值。$n\leq 3000$。
不知道做法是不是对的,反正过了(
假设前缀最大值出现在 $a$,前缀最小值出现在 $b$,设 $a > b$,容易发现答案就是 $sum_a - sum_{b - 1}$。时间反正允许,我们直接枚举 $a, b$,这样我们就需要 $O(1)$ 或 $O(\log n)$ 计算答案。
容易发现我们将 $+k$ 全部放在中间,让两边去平衡,这样显然是最优的。于是就有两个限制:中间的最多只有 $sum + k\times z$,$z$ 表示 0 的个数,两边的限制为 $-sum + k\times z$,因为需要平衡为 0。直接取 $\min$ 即可,时间复杂度 $O(n ^ 2)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| void solve(int l, int r)
{
chkmax(res, std::min(-(sum[n] - sum[r] + sum[l - 1]) + (LL) (cnt[n] - cnt[r] + cnt[l - 1]) * k, sum[r] - sum[l - 1] + (LL) (cnt[r] - cnt[l - 1]) * k));
}
void work()
{
for (int i = 1; i <= n; ++ i)
cnt[i] = cnt[i - 1] + !a[i], sum[i] = sum[i - 1] + a[i];
for (int i = 1; i <= n; ++ i)
for (int j = i; j <= n; ++ j)
solve(i, j);
}
int main()
{
std::cin >> n >> k;
for (int i = 1; i <= n; ++ i) std::cin >> a[i];
int cnt = 0;
LL sum = 0;
for (int i = 1; i <= n; ++ i) cnt += !a[i], sum += a[i];
if (Abs(sum) > (LL) k * cnt) return puts("-1"), 0;
work();
for (int i = 1; i <= n; ++ i) a[i] = -a[i];
work();
std::cout << res + 1 << std::endl;
return 0;
}
|
E
题意:在 $2\times n$ 的网格上,有一些点上有权值 1,每次任选一个 1 向四周移动,注意两个 1 合并后还是一个 1,问最后剩 1 个 1 至少需要多少步。
想了许久,错了很久才发现贪心似乎有问题,写了个 DP 一下就过了。
容易发现我们合并的时候,如果前 $i$ 个有 1 的话,那么消完后一定是只有第一行有 / 只有第二行有一个 1,直接按照这个转移。
具体的,计算第一行的答案,那么答案可以来自 $f(2, i - 1) + 2$,或者是 $f(1, i - 1) + 1+a(2, i)$,因为第二行 $i$ 的位置有 1 的话,那么就需要多一个代价合并到 $f(1, i)$。第二行计算类似,不再赘述。
给出我的错误贪心思路,希望有好心人指出错误 / 给出反例:如果只有 1 行的话,答案显然是最后一个出现的位置减第一个出现的位置 $mx - mn$。这样枚举是最后合并到了第一行还是第二行,然后第二行如果在 $[mn, mx]$ 之间的 1 显然需要 1 个代价合并。旁边多出来的显然需要一次扫描,最后堆在 $mn / mx$ 的位置。这样 $mn, mx$ 如果原来有的话就不再需要多一次操作的,否则需要。错误代码链接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void work()
{
scanf("%d%s%s", &n, s1 + 1, s2 + 1);
int st = 1;
while (s1[st] == '.' && s2[st] == '.') st ++;
f1[st] = s2[st] == '*', f2[st] = s1[st] == '*';
for (int i = st + 1; i <= n; ++ i) {
f1[i] = std::min(f1[i - 1] + (s2[i] == '*') + 1, f2[i - 1] + 2);
f2[i] = std::min(f2[i - 1] + (s1[i] == '*') + 1, f1[i - 1] + 2);
}
int ed = n;
while (s1[ed] == '.' && s2[ed] == '.') ed --;
printf("%d\n", std::min(f1[ed], f2[ed]));
}
|
F
题意:给出一个无向图,要求选出一些关键点,使得每一条边至少有一个端点是关键点,且不超过一条边两个端点是关键点。给出构造,或报告无解。
赛时想到了一些,没写,赛后看到了这个做法,和自己做法有点像,就写贺了一遍。
抽出 dfs 树,如果不考虑可以有一条边两个关键点,那么必须保证所有边两边的深度奇偶性不同,这样按照深度选关键点即可。
现在我们有边可能不满足深度奇偶性不同,那么我们需要调整。具体地就是将一棵子树的选 / 不选状态反转,这样只有连边跨越这棵子树的状态会反转。
首先如果只有一条边不满足条件,直接输出原方案即可(可能不满足条件的边两边都是 0,注意整个翻转)。
注意到一条非树边只有可能是 儿子 - 祖先 的边,设其为 $(v, u)$,那么 $[v, u)$ 的所有点(指 $u, v$ 路径上的所有点,不包括 $u$)之中,需要一个点和他的子树进行翻转。我们将所有的深度奇偶性相同的非树边两边做一次差分,这样再次 dfs,就知道哪些点是可以反转的了。注意两边可能都是 0,所有点需要反转。
具体看代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| void dfs(int x)
{
vis[x] = 1;
for (int i = h[x], v; ~i; i = ne[i])
if (!vis[v = e[i]])
f[v] = x, dep[v] = dep[x] + 1, evis[i >> 1] = 1, dfs(v);
}
void rdfs(int x)
{
for (int i = h[x], v; ~i; i = ne[i])
if (evis[i >> 1] && dep[x] < dep[v = e[i]])
rdfs(v), b[x] += b[v], c[x] += c[v];
}
void dfsans(int x)
{
dep[x] ^= 1;
for (int i = h[x], v; ~i; i = ne[i])
if (evis[i >> 1] && (v = e[i]) != f[x]) dfsans(v);
}
void work()
{
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++ i) vis[i] = 0;
for (int i = 0; i < m; ++ i) evis[i] = 0;
for (int i = 1; i <= n; ++ i) h[i] = -1;
for (int i = 1; i <= n; ++ i) b[i] = c[i] = 0;
idx = 0;
for (int i = 1, u, v; i <= m; ++ i) {
scanf("%d %d", &u, &v);
add(u, v), add(v, u);
}
dfs(1);
int cnt = 0, st, ed;
for (int x = 1; x <= n; ++ x)
for (int i = h[x]; ~i; i = ne[i]) {
if (evis[i >> 1]) continue;
int u = x, v = e[i];
if (dep[u] > dep[v]) continue;
if ((dep[u] - dep[v]) & 1) c[u] --, c[v] ++;
else st = u, ed = v, b[u] --, b[v] ++, cnt ++;
}
rdfs(1);
if (cnt == 1) {
if (!(dep[ed] & 1))
for (int i = 1; i <= n; ++ i) dep[i] ^= 1;
dep[st] = dep[ed] = 1;
puts("YES");
for (int i = 1; i <= n; ++ i) printf("%d", dep[i] & 1);
puts("");
return;
}
int to = -1;
for (int x = 1; x <= n; ++ x)
if (b[x] == cnt && c[x] == 0) {
to = x;
if (dep[x] & 1) {
for (int i = 1; i <= n; ++ i) dep[i] ^= 1;
}
break;
}
if (!~to) return void(puts("NO"));
dfsans(to);
puts("YES");
for (int x = 1; x <= n; ++ x) printf("%d", dep[x] & 1);
puts("");
}
|
