万能欧几里得简介

经典的下取整求和，一般不能使用数论分块等（因为被除数不固定）。

使用类欧几里得的模板题吧（为什么不讲类欧呢？因为感觉没什么用……）。

算法流程

题意：求

$$\sum_{i = 0} ^ n \left\lfloor\dfrac{ai + b}c \right\rfloor$$

$T \leq 10 ^ 5, a, b, c, n\leq 10 ^ 9, c\not= 0$。

看到如此庞大的数据范围，大概率是对数做法了。

将其放在坐标系下，我们可以看作 $y = \dfrac{ax + b}c$，定义这个直线生成的字符串为：越过一个 $x$ 整点，则加一个 R，越过一个 $y$ 整点，则加一个 U，遇到同时的整点先 U 后 R。容易发现这样下去答案一定只和这个字符串有关。

比如对于这个，我们计算答案，即为：遇到 U 则 cnt ++，遇到 R 就 res += cnt。

考虑合并两个已经计算好的答案，我们尝试使用一个结构体维护，容易发现答案需要和前面的 U $cntu$，后面 R 的个数 $cntr$，前后的答案，那么我们可以合并这两个的答案。具体可以写作：

Node operator *(Node a, Node b)
{
	Node res;
	adj(res.u = a.u + b.u - Mod), adj(res.r = a.r + b.r - Mod);
	res.ans = (a.ans + b.ans + LL(a.u) * b.r) % Mod;
	return res;
}

那么我们现在需要做的事情就是将整个序列拆开，最后合并答案。首先我们定义最开始单次向右 R 的结构体 fr 和单次向上 U 的结构体 fu，这样就可以最后合并得到答案。

令最开始的答案为 f(a, b, c, n, fu, fr)，其中 fu 表示向上走一步所乘的结构体，fr 表示向右走一步要成的结构体。注意这里可能不再是开始递归进入的 fu, fr

首先我们考虑第一种情况 $a\geq c$，于是可以将 $a\geq c$ 的变为 $a < c$，具体的，每次 R 前面相当于多加入了 $\left\lfloor\dfrac ac \right\rfloor$ 个 U，那么我们可以直接写作 f(a % c, b, c, n, fu, qpow(fu, a / c) * fr)，qpow 表示快速幂。

那么现在我们需要考虑的就是 $a < c$ 的情况。一个初步的想法是我们现在 $y = \dfrac{ax + b}c$ 的斜率是小于 1 的，我们可以将 $x, y$ 交换一下，将 fu, fr 交换一下，这样就可以将斜率变为大于 1 的情况，从而可以继续递归。

我们显然可以变形为 $x = \dfrac{cy - b}{a}$（为了清楚，这里只是对式子进行了变形，没有把 $x, y$ 交换）。但是我们需要注意有 U 和 R 的优先级的问题。比如下图：

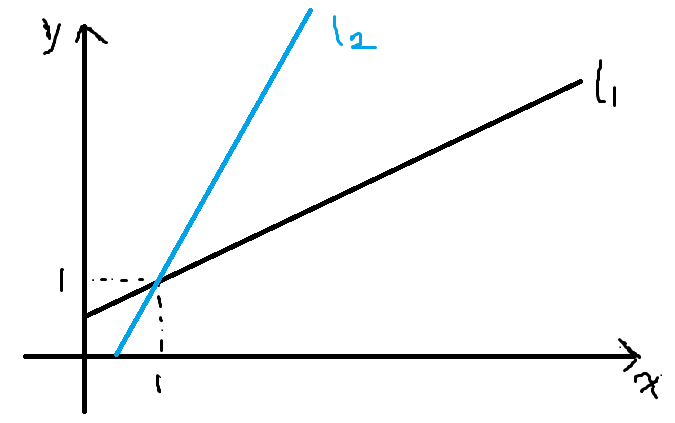
原来的线经过了 $(1, 1)$，是先 U 后 R，但是翻转之后，变成了先 R 后 U，所以我们需要将这条线向右平移 $\dfrac 1a$ 个单位，这样就是先 U 后 R，对应上了原来的字符串。

于是我们现在需要计算的就是 $x = \dfrac{cy - b - 1}a$ 的答案。注意我们现在这个的定义域是 $(0, n]$，即我们需要计算最开始的 fu 贡献，但不计算最开始 fr 的贡献。所以可以得到 $b$ 是属于 $[0, c - 1]$ 的。

回到上面那张图，我们发现 $(0, 1]$ 的部分的答案是不完整的，我们不能直接扔给下一个算，那么前面所经过的 $\left\lfloor\dfrac{c - b - 1} a \right\rfloor$ 个 fu 是需要提前乘入的，另外还有一个 fr。

然后我们考虑 $(1, \left\lfloor\dfrac{an + b}c \right\rfloor]$ 这段区间如何计算。容易发现这就是我们需要递归的部分，但是注意，我们计算的定义域是 $(0, n]$，所以需要我们向左平移一个单位得到 $x = \dfrac{cy + c - b - 1}{a}$，所以应该递归到 f(c, c - b - 1, a, m - 1, fr, fu)（$m = \left\lfloor\dfrac{an + b}c \right\rfloor$）。

最后我们需要考虑 $y > m, x\leq n$，这样我们转化一下就是 $x\in (\left\lfloor\dfrac{cm - b - 1}a \right\rfloor, n]$，容易发现我们需要乘上 qpow(fu, n - (c * m - b - 1) / a)。

那么我们就可以得到最后的 AsGcd 代码为：

Node AsGcd(int a, int b, int c, int n, Node fu, Node fr)
{
	b %= c;
	if (a >= c) return AsGcd(a % c, b, c, n, fu, qpow(fu, a / c) * fr);
	LL m = (LL(a) * n + b) / c;// y = (cx - b - 1) / a
	if (m == 0) return qpow(fr, n);// all is fr
	std::swap(fu, fr);
	return qpow(fu, (c - b - 1) / a) * fr // solving x in [0, 1]
	* AsGcd(c, c - b - 1, a, m - 1, fu, fr) // solving x in (1, m]
	* qpow(fu, n - (c * m - b - 1) / a) // solving x in [m, m + 1), notice that y_max = n
	;
}

类似欧几里得算法，得到时间复杂度 $O(\log(a + c))$，不过常数比较大。

最后递归的时候，注意到 0 是被包含进入答案的，所以递归前，我们要先乘上 qpow(fu, b / c) * fr。

例题

给定 $a, b, c, l$ 和 $n\times n$ 的矩阵 $A, B$，求：

$$\sum_{i = 1} ^ l A ^ {i} B ^ {\lfloor\frac{ai + b}{c} \rfloor}$$

$a, b, c, \lfloor\dfrac{al + b}{c}\rfloor\leq 10 ^ {18}$。

通过这个题，我们就可以看出万能欧几里得的优势：只需要将上面的模板记住（或手推），然后处理一下信息的合并即可。这相对于类欧几里得优化了许多，思维量减小了不少。

看这个题，如果我们需要合并两个已经计算好的信息，我们需要维护 $A ^ x$，这就是后面的答案需要乘在前面的；然后还需要维护 $B ^ {\lfloor\frac {ax + b}c \rfloor}$，这个需要乘在答案的中间，这和乘在最后没有区别。

于是我们需要维护三个信息，而这三个信息是可以用 $O(n ^ 3)$ 时间合并的。

struct Node {
	Matrix cntx, cnty, ans;
};

Node operator *(Node a, Node b)
{
	a.ans += a.cntx * b.ans * a.cnty;
	a.cnty = a.cnty * b.cnty, a.cntx = a.cntx * b.cntx;
	return a;
}

这样我们套用前面的计算方法直接复制，得到这份代码：

Node AsGcd(LL a, LL b, LL c, LL n, Node fu, Node fr)
{
	b %= c;
	if (a >= c) return AsGcd(a % c, b, c, n, fu, qpow(fu, a / c) * fr);
	LL m = ((s128) a * n + b) / c;
	if (m == 0) return qpow(fr, n);
	std::swap(fu, fr);
	auto ret = qpow(fu, (c - b - 1) / a) * fr * AsGcd(c, c - b - 1, a, m - 1, fu, fr)
		* qpow(fu, n - ((s128) c * m - b - 1) / a);
	return ret;
}

最后我们需要考虑的就是一个 U 和一个 R 分别产生什么影响。

一个 U 会使得 cnty ++，而 $cntx$ 不变；一个 R 会使得 cntx ++，ans += cntx，$cnty$ 不变。而一个单位元就是 cntx = cnty = 0（注意我这里是使用 $A, B$ 的多少次方表示的，所以 cntx = 0 表示的是单位矩阵，以此类推）。

那么 fu = {I, B, 0}, fr = {A, I, A} 表示 U 和 R 分别带来的影响。

前面照例乘上一个 qpow(fu, b / c)，注意从 1 开始，不需要乘 fr。

struct Node {
	Matrix cntx, cnty, ans;
} f0;

Node operator *(Node a, Node b)
{
	a.ans += a.cntx * b.ans * a.cnty;
	a.cnty = a.cnty * b.cnty, a.cntx = a.cntx * b.cntx;
	return a;
}

Node qpow(Node a, LL k)
{
	assert(k >= 0);
	Node res(f0);
	for (; k; k >>= 1, a = a * a)
		if (k & 1) res = res * a;
	return res;
}

Node AsGcd(LL a, LL b, LL c, LL n, Node fu, Node fr)
{
	b %= c;
	if (a >= c) return AsGcd(a % c, b, c, n, fu, qpow(fu, a / c) * fr);
	LL m = ((s128) a * n + b) / c;
	if (m == 0) return qpow(fr, n);
	std::swap(fu, fr);
	auto ret = qpow(fu, (c - b - 1) / a) * fr * AsGcd(c, c - b - 1, a, m - 1, fu, fr)
		* qpow(fu, n - ((s128) c * m - b - 1) / a);
	return ret;
}

int main()
{
	LL a, b, c, l;
	std::cin >> a >> c >> b >> l >> n;
	for (int i = 0; i < n; ++ i) I[i][i] = 1;
	for (int i = 0; i < n; ++ i)
		for (int j = 0; j < n; ++ j) scanf("%d", &A[i][j]);
	for (int i = 0; i < n; ++ i)
		for (int j = 0; j < n; ++ j) scanf("%d", &B[i][j]);
	Node fu{I, B, {}}, fr{A, I, A};
	f0 = {I, I, {}};
	auto res = (qpow(fu, b / c) * AsGcd(a, b, c, l, fu, fr)).ans;
	for (int i = 0; i < n; ++ i, puts(""))
		for (int j = 0; j < n; ++ j) printf("%d ", res[i][j]);
	return 0;
}