经典容斥。
题意:有 $2 ^ n$ 个选手进行淘汰赛,比赛时编号小的会获胜,但是当 1 号选手遇到给定 $m$ 位选手中的任意一个,他将会输掉比赛。问怎样合理的安排顺序,使得 1 号选手能获胜。$n, m\leq 16$。
首先 1 号选手的位置在 $[1, 2 ^ n]$ 中任意位置是一样的,所以最后答案乘上 $2 ^ n$。
然后其实很多的排法,我们只关心其中 $n$ 棵子树的最小值即可,并不关心是如何排布的。如下图,我们只需要关心蓝色子树的最小值即可。
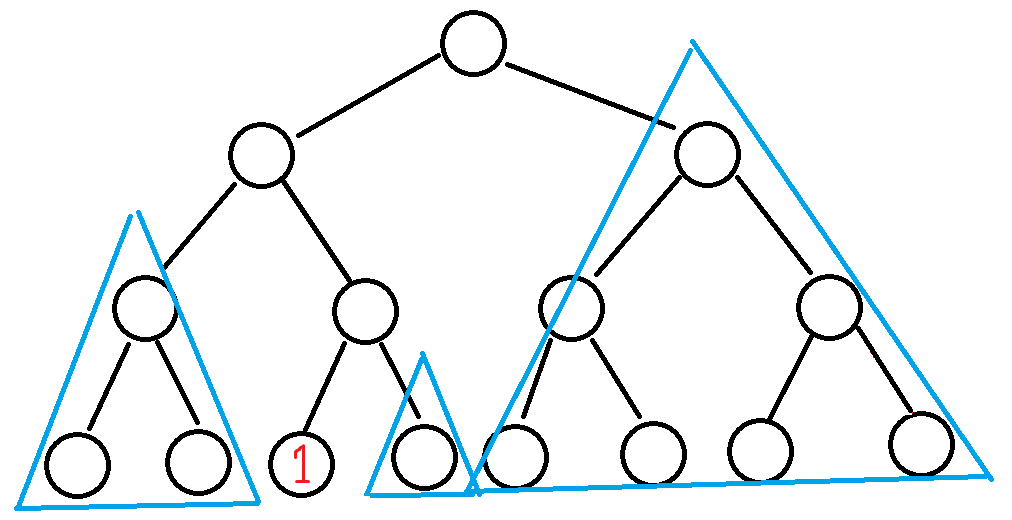
考虑容斥,题目要求这些子树的最小值中不能出现 $m$ 个数中的一个,那么考虑钦定其中 $k$ 个子树最小值是 $m$ 个数当中的,贡献乘上 $(-1) ^ k$。
如果我们要钦定大小为 $sz$ 的子树的最小值为 $v$,注意钦定的时候我们剩下的 $sz - 1$ 个都要严格大于 $v$。
注意如果我们乱序加入 $v$ 的话,我们其实是并不知道大于 $v$ 的有多少个。类似于 LOJ3119 随机正方体 的方式,我们倒序枚举 $v$ 加入,这样枚举到 $v$ 的时候,前面所有钦定的一定都是大于 $v$ 的,就避免了大于 $v$ 的个数不确定的情况。随便状态压缩一下,记录哪些 $sz$ 已经钦定了最小值即可,转移时乘一下组合数,最后注意排列顺序即可。时间复杂度 $O(mn2 ^ n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| int main()
{
init();
int n, m;
std::cin >> n >> m;
std::vector<int> usd(m);
for (int &x : usd) scanf("%d", &x);
std::sort(usd.begin(), usd.end());
f[m + 1][0] = 1;
for (int i = m; i; -- i)
for (int s = 0; s < (1 << n); ++ s)
{
if (!f[i + 1][s]) continue;
adj(f[i][s] += f[i + 1][s] - Mod);
for (int j = 0; j < n; ++ j)
if (!(s >> j & 1))
f[i][s | (1 << j)] = (f[i][s | (1 << j)] + (LL)
C((1 << n) - usd[i - 1] - s, (1 << j) - 1) * (Mod - f[i + 1][s])) % Mod;
}
int res = 0;
for (int s = 0; s < (1 << n); ++ s)
{
int mul = 1;
for (int i = 0; i < n; ++ i)
if (s >> i & 1) mul = (LL) mul * fact[1 << i] % Mod;
res = (res + (LL) f[1][s] * mul % Mod * fact[(1 << n) - 1 - s]) % Mod;
}
res = res * (1LL << n) % Mod;
std::cout << res << std::endl;
return 0;
}
|
