AT Code Festival 2017 Qual A F Squeezing Slimes

有趣的结论题。

题意：目前有 $\sum_{i = 1} ^ n a_i$ 个 1，每次可以选定一个长度为 $2m$ 的区间，然后 1、2 合并，3、4 合并，最后剩下 $m$ 个数，称为一次操作。问最少多少次操作使得该序列变为 $a$。$n\leq 10 ^ 5$，$a_i\leq 10 ^ 9$。

题目传送门 AtCoder

正向不好做，考虑逆向变换。假设 $x$ 为当前这个处理的数，设 $c$ 为最大的满足 $2 ^ c \leq x$ 的数，如果 $2 ^ c = x$，那么我们可以把 $c$ 次操作和前后都一起分裂，否则的话，我们需要另外一次操作，且只能和一边一起分裂。

画一个分解 5 的图理解：

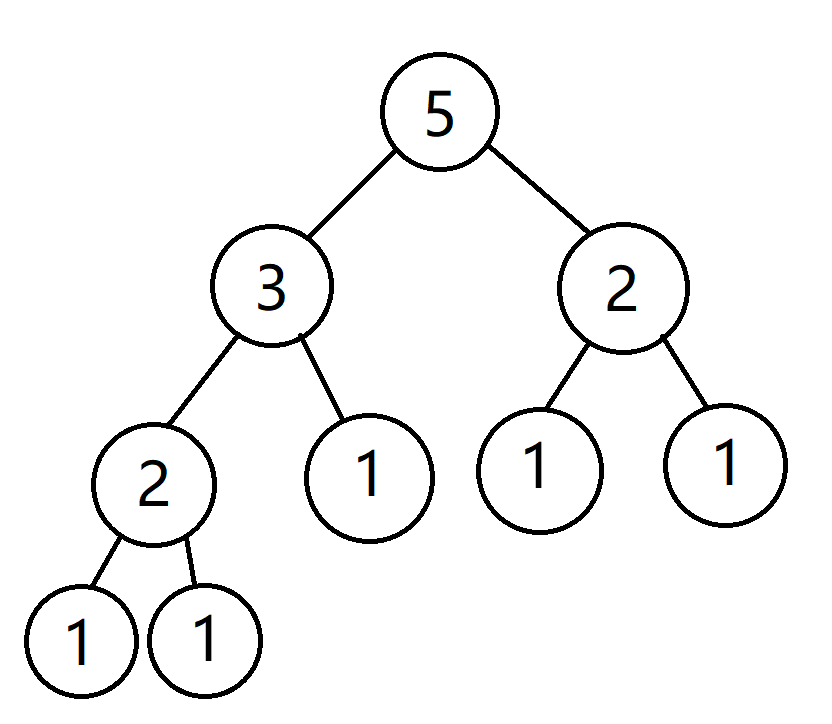
这样我们前两次分裂操作都可以和前面和后面同步，但最后一次操作只能和前面同步（也可以翻转和后面同步）。

按序扫描 $a$，记录 $ls$ 表示前面能传过来的操作次数。如果 $ls < c$，那么我们需要额外的 $c - ls$ 操作来补齐，否则不需要。另外，如果需要额外的操作，如果 $ls > c$，我们可以选择与前面一起分裂，否则重新开一次操作，$ls$ 也加 1。

int main()
{
	int n, ls = 0, res = 0, x, cur;
	std::cin >> n;
	while (n --)
	{
		scanf("%d", &x), cur = std::log(x) / std::log(2);
		bool flag = (1 << cur) != x;
		if (ls <= cur) res += cur - ls;
		else flag = false;
		ls = cur;
		if (flag) ls ++, res ++;
	}
	std::cout << res << '\n';
	return 0;
}