mydcwfy's Blog

ARC Round#141

Posted on
Symbols count in article: 4.9k Reading time ≈ 11 mins.

有趣的比赛，做题 + 改题一共交了 35 次……

A、B 略去。

C

题意：有一个括号序列 $S$，在 $[1, 2n]$ 的所有排列中，对应括号序列合法且最小的排列记为 $P$，对应括号序列合法且最大的排列记为 $Q$，已知 $P, Q$，求 $S$ 或报告无解。$n\leq 2\times 10 ^ 5$。

首先如果 $P_{2i - 1} > P_{2i}$ 的话，那么 $S_{P_{2i - 1}}$ 一定是 (，而 $S_{P_{2i}}$ 一定是 )，否则我们一定可以交换 $P_{2i - 1}$ 和 $P_{2i}$。$Q$ 能确定的为如果 $Q_{2i - 1} < Q_{2i}$ 的话，那么 $Q_{2i - 1}$ 一定是 (，$Q_{2i}$ 一定是 )，证明同理。

考虑一下结论：

结论：如果在这时还有多个 $S$ 合法的话，那么就没有合法的 $S$。

证明：首先假设有合法的 $S$。容易发现一个括号序列一定是由一些合法的括号序列或者是合法的括号序列翻转后拼接得到的。我们先只考虑 $S$ 是合法的括号序列的情况。那么我们假设 ( 出现的位置是 $L_{1\cdots n}$，) 出现的位置是 $R_{1\cdots n}$，显然有 $L_1 < R_1, L_2 < R_2, \cdots$，那么 $Q$ 的排列一定是 $(L_n, R_n, L_{n - 1}\cdots)$。按照刚刚的构造方法，我们可以根据 $Q$ 还原出唯一的 $S$（$L_n < R_n$ 可以还原 $S_{L_n}$ 是 (，$S_{R_n}$ 是 )，一起类推）。翻转过来我们可以通过 $P$ 类似的唯一还原 $S$。

注意到一个合法括号序列一定长度是偶数，那么其实我们只需要比较 $P_{2i - 1}$ 和 $P_{2i}$，就可以维护还原 $S$。而反之如果我们不能还原唯一的 $S$，那么就一定都不合法。

这样我们只需要根据现有的限制随便构造一组解，然后用 $S$ 还原 $P, Q$，看一下 $S$ 是否合法即可。（注意不是 $P, Q$ 分别还原 $S$ 比较）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
void fail() { puts("-1"), exit(0); }
 
void force(int pos, int val)
{
	if (a[pos] == (val ^ 1)) fail();
	a[pos] = val;
}
 
int main()
{
	std::cin >> n;
	for (int i = 1; i <= n * 2; ++ i) scanf("%d", p + i);
	for (int i = 1; i <= n * 2; ++ i) scanf("%d", q + i);
	memset(a, -1, sizeof(a));
	for (int i = 1; i < 2 * n; i += 2)
		if (p[i] > p[i + 1]) force(p[i], 1), force(p[i + 1], 0);
	for (int i = 1; i < 2 * n; i += 2)
		if (q[i] < q[i + 1]) force(q[i], 1), force(q[i + 1], 0);
	for (int i = 1, op = 0; i <= 2 * n; ++ i)
		if (!~a[p[i]]) a[p[i]] = op = op ^ 1;
	for (int i = 1; i <= 2 * n; ++ i) vis[i] = false;
	for (int i = 1, j = 1, tot = 0, top = 0; i <= 2 * n; ++ i)
	{
		if (!top) {
			while (j <= 2 * n && (vis[j] || !a[j])) ++ j;
			vis[chkp[++ tot] = j] = true, top ++;
		}
		if (!vis[i]) vis[chkp[++ tot] = i] = true, top += a[i] ? 1 : -1;
	}
	for (int i = 1; i <= 2 * n; ++ i)
		if (p[i] != chkp[i]) fail();
 
	for (int i = 1; i <= 2 * n; ++ i) vis[i] = false;
	for (int i = 2 * n, j = 2 * n, tot = 0, top = 0; i; -- i)
	{
		if (!top) {
			while (j && (vis[j] || !a[j])) -- j;
			vis[chkp[++ tot] = j] = true, top ++;
		}
		if (!vis[i]) vis[chkp[++ tot] = i] = true, top += a[i] ? 1 : -1;
	}
	for (int i = 1; i <= 2 * n; ++ i)
		if (q[i] != chkp[i]) fail();
 
	for (int i = 1; i <= 2 * n; ++ i) putchar(a[i] ? '(' : ')');
	return 0;
}

D

题意：给定一个 $n$ 个数的集合 $S$，每一个数都 $\leq 2m$，问对于每一个数，当选定这一个数后，还能不能选出一个大小为 $m$ 的集合（加上选出的这个数），使得集合内部没有倍数关系。$n, m\leq 2\times 10 ^ 5$。

注意到恰好大小为 $m$，而所有数都满足 $\leq 2m$。什么东西恰好有 $m$ 个呢？这里就要用到构造，恰好有 $m$ 个奇数。我们把每个数按照 $a\times 2 ^ b$（$a$ 为奇数）拆分，然后塞到 $a$ 这个桶内部。容易发现 $m$ 个桶，每个桶都最多只有一个数被选。那么如果出现一个桶没有数，就一定没有解。否则假设选出来的数的 2 的次幂为 $v_i$。

此外，不同桶之间还可能存在倍数关系，比如 $a\times 2 ^ x$ 是 $b\times 2 ^ y$ 的倍数当且仅当 $b|a$ 并且 $x\geq y$。那么对于成倍数的 $(a, b)$ 的 std::pair，那么一定需要保证 $v_a < v_b$。

如何判断一个数能否出现在合法的集合中呢？我们可以考虑对于每一个 $i$，计算 $v_i$ 的区间。具体的，如果需要计算最大值的话，顺序扫一遍，计算完一个数后更新他的倍数。计算最小值的时候倒序扫一遍，计算这个数的最小值时从他的倍数更新过来。复杂度都是 $O(m\log m)$ 的。

最后来一个数判一判在不在区间里即可。注意这个区间的上界和下界对应的数都是存在于原来的集合的，否则整个都无解。

赛后改题唯一一个 1 遍过的题目，其他的题目都不知错了多少发。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void fail() {
	while (n --) puts("No");
	exit(0);
}
 
int main()
{
	std::cin >> n >> m;
	for (int i = 1; i <= n; ++ i) scanf("%d", a + i);
	for (int i = 1; i <= n; ++ i) g[a[i] >> ctz(a[i])].push_back(ctz(a[i]));
	for (int i = 1; i <= 2 * m; ++ i)
	{
		if (!(i & 1)) continue;
		int j = i;
		while (j <= m) j <<= 1, R[i] ++;
	}
	for (int i = 1; i <= 2 * m; ++ i) L[i] = -1e9;
	for (int i = 1; i <= 2 * m; ++ i)
	{
		if (!(i & 1)) continue;
		if (g[i].empty() || g[i].front() > R[i]) fail();
		R[i] = *-- std::upper_bound(g[i].begin(), g[i].end(), R[i]);
		for (int d = 2; d * i <= 2 * m; ++ d) chkmin(R[i * d], R[i] - 1);
	}
	for (int i = 2 * m; i; -- i)
	{
		if (!(i & 1)) continue;
		for (int d = 2; d * i <= 2 * m; ++ d) chkmax(L[i], L[i * d] + 1);
		// std::cout << i << ' ' << L[i] << ' ' << g[i].back() << '\n';
		if (g[i].empty() || g[i].back() < L[i]) fail();
		L[i] = *std::lower_bound(g[i].begin(), g[i].end(), L[i]);
	}
	
	for (int i = 1; i <= n; ++ i)
	{
		int y = ctz(a[i]), x = a[i] >> y;
		if (y >= L[x] && y <= R[x]) puts("Yes");
		else puts("No");
	}
	return 0;
}

E

题意：给定一个 $n\times n$ 的网格，标号从 0 开始，$m$ 次给定 $a, b, c, d$，把 $((a + i)\bmod n, (b + i)\bmod n)$ 和 $((c + i)\bmod n, (d + i)\bmod n)$ 连接起来，每次操作后问连通块数目。$n, m\leq 2\times 10 ^ 5$。

容易发现按照 $(b - a)\bmod n$ 分类，然后使用并查集，这样连边的时候相当于只是在 2 个集合中间按照一定的 $\Delta$ 量连边。这样考虑怎怎样动态维护这个 $\Delta$ 量。

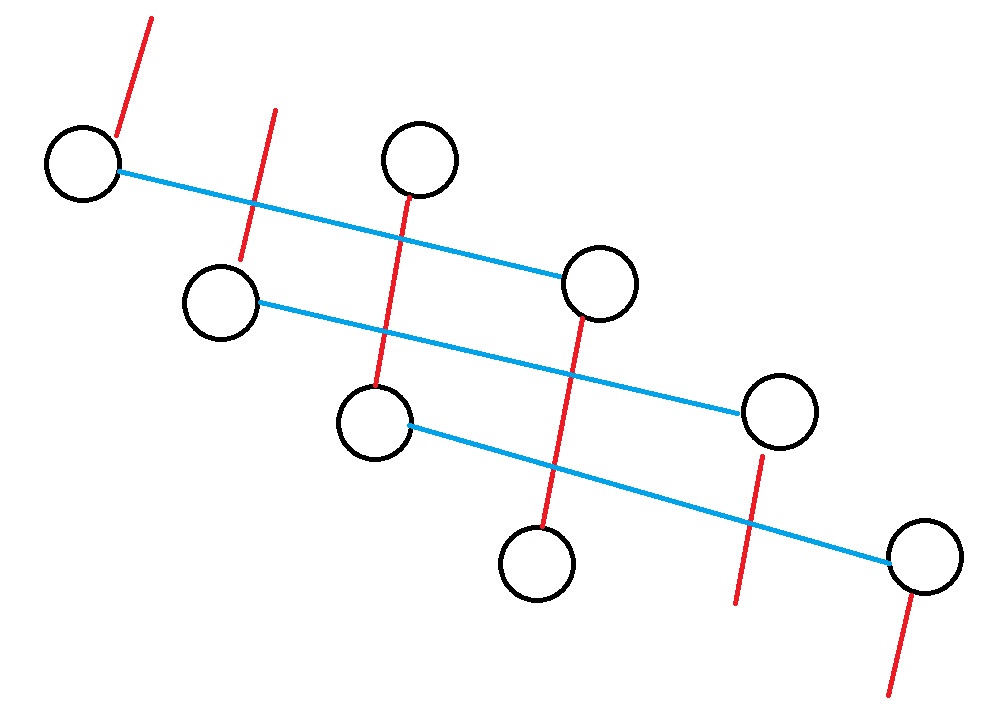
首先显然需要维护该集合到根所代表的集合，其 $\Delta$ 是多少（即 根的 $(0, x)$ 连到该集合的 $(\Delta, \Delta + y)$）。然后可能出现连边两个原来就联通的集合，那么我们注意，并不一定是毫无用处，比如：

这样蓝边后加入，虽然没有改变不同集合联通性，但是我们发现，一个集合内部出现的连边，他们每 3 个就连在了一起。于是我们还需要维护该集合内部循环长度是多少。两个合并的时候，其实就是 $\gcd$，手玩一下即可。循环长度也就是该集合总共的连通块个数，直接维护答案变化即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int find(int x)
{
	if (x == f[x]) return x;
	int rt = find(f[x]);
	dis[x] = (dis[x] + dis[f[x]]) % del[rt];
	return f[x] = rt;
}
 
int main()
{
	std::cin >> n >> m;
	for (int i = 0; i < n; ++ i) f[i] = i;
	for (int i = 0; i < n; ++ i) del[i] = n;
	LL ans = (LL) n * n;
	int a, b, c, d;
	while (m --)
	{
		scanf("%d %d %d %d", &a, &b, &c, &d);
		int x = (b - a + n) % n, y = (d - c + n) % n, de = (d - b + n) % n,
			fx = find(x), fy = find(y);
		if (fx == fy) {
			ans -= del[fx];
			del[fx] = Gcd(del[fx], dis[x] - dis[y] + del[fx] + de);
			ans += del[fx];
		} else {
			ans -= del[fx] + del[fy];
			del[fx] = Gcd(del[fx], del[fy]);
			f[fy] = fx, dis[fy] = (dis[x] - dis[y] + n + de) % del[fx];
			ans += del[fx];
		}
		printf("%lld\n", ans);
	}
	return 0;
}

F

见 ARC141F