mydcwfy's Blog

LOJ2268 [SDOI2017]苹果树

Posted on
Symbols count in article: 3k Reading time ≈ 7 mins.

题意：有一棵 $n$ 个点的有根树，每个点有 $a_i$ 个苹果，在 $i$ 处选一个苹果的价值是 $v_i$，一个节点能选苹果当且仅当他的父亲也选了至少一个。假设选的最大深度是 $d$，选了 $t$ 个苹果，要求 $t - d\leq k$，$k$ 给定。求能获得的最大价值。$T(T\leq 5)$ 组数据，$n\leq 2\times 10 ^ 4$，$ k\leq 5\times 10 ^ 5$，$nk\leq 2.5\times 10 ^ 7$，$1\leq v_i\leq 100$，5s。

容易发现题目直接给了个 $nk\leq 2.5\times 10 ^ 7$，那么显然复杂度就是 $O(nk)$，在多重背包的时候还必须使用单调队列优化。另外，不能使用任何的背包合并，因为复杂度为 $O(k ^ 2)$，唯一能合并的只是最后我们只需要一个答案，可以在 $O(k)$ 时间合并。那么我们必须找到两个背包合并得到答案。

首先容易发现一个事实：我们肯定会去选叶子节点。因为我们不选的话，让他任意选择一个儿子一定不劣。然后我们会发现一个树被我们用这一条根到叶子的链划分成了三部分：

  1. 根到叶子的链
  2. 该链的左边
  3. 该链的右边

这个左右暂且不好定义，我们先放在这里。容易发现我们根到叶子的链如果都只选择一个的话，这条链本身是免费的（不需要代价），如果要多选的话，我们可以考虑把这个点建一个新儿子，存放 $a_i - 1$ 个苹果。这个节点一定在链的左边或者右边（废话），那么就当作其他节点计算了。容易发现这个贡献方法是正确的。

首先我们考虑如何表示该链的左边和右边。这里巧妙的运用到了 dfn 序。考虑正向遍历邻接表和逆向遍历邻接表的后序遍历：

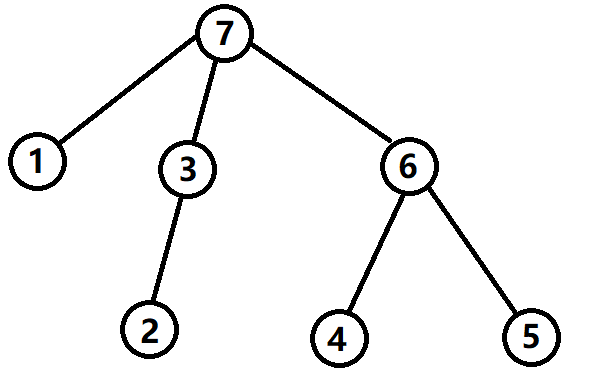
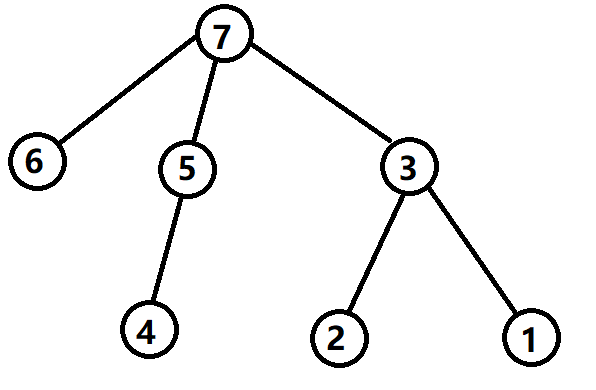
（注意这里没有新加的一个儿子）

假设我们考虑第一个图中 dfn 序为 2 的点，容易发现他的左边的点就是 dfn 序为 $[1, 1]$ 的区间。在第二个图中的 dfn 序为 4，$[1, 3]$ 区间的点就是他右边的点。

现在我们对树的左边和右边的定义就比较清晰了，我们预处理出这两个背包，然后 $O(k)$ 合并即可。

最后一个问题就是怎样求一段区间 dfn 序的树上背包。对于一个节点，可以强制至少选一个，否则的话需要跳过一个整的子树。这个是一个多重背包，显然 $O(nk)$ 即可。

综上，时间复杂度 $O(nk)$，可以通过，但比较卡常。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
void chkpack(std::vector<int> &f, std::vector<int> &g) { for (int i = 0; i <= lim; ++ i) chkmax(f[i], g[i]); }

void backpack(std::vector<int> &f, int w, int v, bool flag = false)
{
	if (!w) return;
	// std::cout << "backPack " << w << ' ' << v << std::endl;
	static int q[M];
	std::vector<int> tmp(lim + 1);
	int hh = 1, tt = 0;
	for (int i = 0; i <= lim; ++ i)
	{
		while (hh <= tt && i - q[hh] > w) hh ++;
		if (hh <= tt) {
			if (flag) tmp[i] = f[q[hh]] + (i - q[hh]) * v;
			else chkmax(tmp[i], f[q[hh]] + (i - q[hh]) * v);
			// chkmax(f[i], f[q[hh]] + (i - q[hh]) * v);
		} else if (flag) tmp[i] = -INF;
		while (hh <= tt && f[q[tt]] - q[tt] * v < f[i] - i * v) tt --;
		q[++ tt] = i;
	}
	f.swap(tmp);
}

void dfs1(int x, int pre = 0)
{
	sz[x] = 1, sum[x] = (pre += val[x]);
	for (int v : g[x]) dfs1(v, pre), sz[x] += sz[v];
	nw1[dfn1[x] = ++ *dfn1] = x;
}

void dfs2(int x)
{
	for (int v : g[x]) dfs2(v);
	nw2[dfn2[x] = ++ *dfn2] = x;
}

void work()
{
	std::cin >> n >> lim;
	for (int i = 1; i <= n; ++ i) scanf("%d %d %d", &fa[i], &a[i], &val[i]);
	int _n = n;
	for (int i = 1; i <= n; ++ i)
		fa[++ _n] = i, a[_n] = a[i] - 1, val[_n] = val[i], a[i] = 1;
	pren = n, n = _n;
	for (int i = 1; i <= n; ++ i) g[i].clear();
	for (int i = 1; i <= n; ++ i) g[fa[i]].push_back(i);
	*dfn1 = 0, dfs1(1);
	for (int i = 1; i <= n; ++ i) std::reverse(g[i].begin(), g[i].end());
	*dfn2 = 0, dfs2(1);
	pre1[0].assign(lim + 1, -INF), pre2[0].assign(lim + 1, -INF);
	pre1[0][0] = pre2[0][0] = 0;
	for (int i = 1; i <= n; ++ i)
		backpack(pre1[i] = pre1[i - 1], a[nw1[i]], val[nw1[i]], true), chkpack(pre1[i], pre1[i - sz[nw1[i]]]);
	for (int i = 1; i <= n; ++ i)
		backpack(pre2[i] = pre2[i - 1], a[nw2[i]], val[nw2[i]], true), chkpack(pre2[i], pre2[i - sz[nw2[i]]]);
	/*for (int i = 1; i <= n; ++ i) std::cout << nw1[i] << ' ';
	std::cout << '\n';
	for (int i = 1; i <= n; ++ i, std::cout << '\n')
		for (int j = 0; j <= lim; ++ j) std::cout << pre1[i][j] << ' ';*/
	int res = 0;
	for (int i = 1; i <= pren; ++ i)
		if (g[i].size() == 1)
			for (int j = 0; j <= lim; ++ j) chkmax(res, sum[i] + pre1[dfn1[i] - 2][j] + pre2[dfn2[i] - 1][lim - j]);
	std::cout << res << '\n';
}