mydcwfy's Blog

LOJ3704 「联合省选 2022」序列变换

Posted on
Symbols count in article: 3.3k Reading time ≈ 7 mins.

题意：给定一个长度为 $2n$ 的合法括号序列，每个左括号有一个权值，每次你可以把 $p(A)(B)q$ 改成 $p(A()B)q$ 的形式，代价为 $(A)$ 的第一个左括号乘 $x$ 加上 $(B)$ 的第一个左括号乘 $y$（$A, B$ 必须是合法括号序列，$p, q$ 无限制），或者任意交换相邻的合法括号序列，不需要代价。问最少需要多少代价才能使得括号序列不包含 $()()$ 的结构。$n\leq 4\times 10 ^ 5$，$0\leq x, y\leq 1$，$a_i\leq 10 ^ 7$。

考虑我们用括号树来刻画这个变换。首先将括号转成树的方法是一对括号代表一个节点，然后内部的都是在他子树内部的。那么我们可以用图表示这个变化过程：

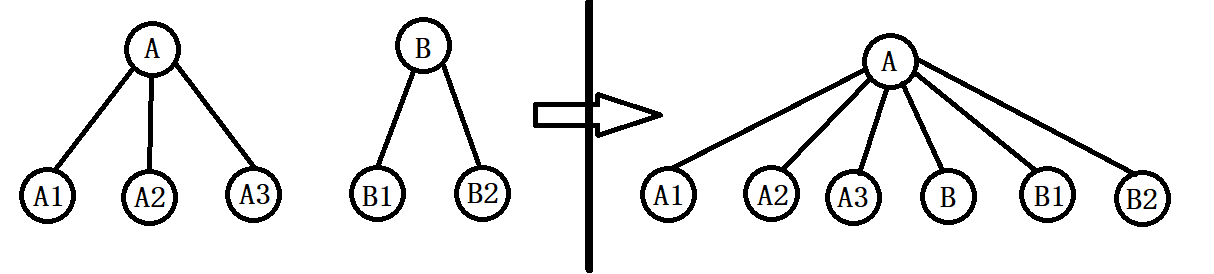
由图可以看出我们相当于用 A 把 B push 到了下一层，实际上其他的都没有变化。由于我们最后需要把整棵树变成一条链，所以其实中间的父子关系其实是没有关系的，我们只关心每个点所在的层数。

x = 0，y = 0

答案显然为 0。

x = 0，y = 1

这个相当于我们需要计算 B 的贡献，那么显然我们需要把最大的留在本层，这样代价尽量小。用一个 std::multiset 暴力维护即可做到 $O(n\log n)$。

x = 1，y = 1

我们计算的单层答案就是 $mn\times (sz - 2) + sum$，容易发现还是把最大的保留在当前层即可。复杂度仍然是 $O(n\log n)$。

x = 1，y = 0

现在我们计算的单层答案就是 $mn\times (sz - 2) + w$，$w$ 表示最后留下的权值。注意到除了最后一层的权值以外，其他的权值都被 $w$ 算了一遍。那么我们可以枚举最后一层的权值，这样的话剩下的就和前面的差不多，把最大的保留在当层即可，复杂度 $O(n ^ 2\log n)$。

注意到如果当前层个数 $\geq 3$ 的话，我们容易发现最大值和最小值都是有意义的，因为最小值可以让后面层贡献减少，而保留最大值到最后一层也是好的。难点在于我们对于个数 $=2$ 的情况 push 谁。

注意到一个性质就是 $sz$ 一定形如一个单峰的形式，而且下降一定是每次减 1。也就是说 $sz = 2$ 一定出现在前缀一段和倒数第二层。倒数第二层显然下放最大值，那么前面的应该怎么下放呢？

注意到我们前面说到只有最小值和最大值是有意义的，这一段 $sz = 2$ 最后只会下放一个值，那么这个值一定是最大值或者最小值。两个分别做就好了。复杂度 $O(n\log n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
LL solve(int st, int v)
{
    std::multiset<int> ms;
    LL ret = 0;
    bool flag = false;
    for (int i = 1; i < n; ++ i)
    {
        for (int x : allv[i]) ms.insert(x);
        ret += ((LL) ms.size() - 2) * *ms.begin();
        if (ms.size() >= 3 || flag) {
        	ret += *-- -- ms.end();
        	ms.erase(-- -- ms.end());
        	flag = true;
        	continue;
        }
        if (i >= st && v == *ms.rbegin()) {
            if (ms.size() == 1) return 1e18;
            ret += *++ ms.rbegin(), ms.erase(-- -- ms.end());
        }
        else ret += *ms.rbegin(), ms.erase(-- ms.end());
    }
    return ret;
}

int main()
{
#ifndef Fly727
    freopen("bracket.in", "r", stdin);
    freopen("bracket.out", "w", stdout);
#endif
    scanf("%d%d%d%s", &n, &x, &y, s + 1);
    for (int i = 1; i <= n; ++ i) scanf("%d", a + i);
    for (int i = 1, c = 0, t = 0; i <= 2 * n; ++ i)
        if (s[i] == '(') allv[++ c].insert(a[++ t]), deg[t] = c;
        else -- c;
    if (x == 0 && y == 0) return puts("0"), 0;
    if (AllSame::issub()) return AllSame::solve(), 0;
    if (x == 0 && y == 1) {
        std::multiset<int, std::greater<int>> ms;
        LL sum = 0, res = 0, cur;
        for (int i = 1; i <= n; ++ i)
        {
            for (int x : allv[i]) ms.insert(x), sum += x;
            cur = *ms.begin(), ms.erase(ms.begin()), sum -= cur;
            res += sum;
        }
        std::cout << res << '\n';
        return 0;
    }
    if (x == 1 && y == 1) {
        std::multiset<int, std::greater<int>> ms;
        LL sum = 0, res = 0, cur;
        for (int i = 1; i <= n; ++ i)
        {
            for (int x : allv[i]) ms.insert(x), sum += x;
            res += sum + *-- ms.end() * ((int) ms.size() - 2);
            cur = *ms.begin(), ms.erase(ms.begin()), sum -= cur;
        }
        std::cout << res << '\n';
        return 0;
    }
    LL res = solve(n, 0);
    bool flag1 = true, flag2 = false;
    int edeg = 0, v = 0;
    for (int i = 1, t = 0; i < n; ++ i)
    {
        t += allv[i].size();
        flag1 &= t <= 2, flag2 |= t >= 2;
        if (flag1 && flag2 && allv[i].size() && chkmax(v, *allv[i].rbegin())) edeg = i;
        t --;
    }
    chkmin(res, solve(edeg, v));
    // std::cout << edeg << ' ' << v << '\n';
    v = 1e9, flag1 = true, flag2 = false;
    for (int i = 1, t = 0; i < n; ++ i)
    {
        t += allv[i].size();
        flag1 &= t <= 2, flag2 |= t >= 2;
        if (flag1 && flag2 && allv[i].size() && chkmin(v, *allv[i].begin())) edeg = i;
        t --;
    }
    chkmin(res, solve(edeg, v));
    // std::cout << edeg << ' ' << v << '\n';
    std::cout << res << '\n';
    return 0;
}